모델 학습에 필요한 최적화에 대해 알아본다. 우리가 머신러닝 모델을 학습한다는 것은 주어진 데이터로 설명할 수 있는 목적함수를 기준으로 이 함수 값을 가장 작게 하는 모델 파라미터를 찾게하는 과정이다.
여기서는 목적함수 값을 최소화시켜주는 (최적화하는) 알고리즘에 대해 알아본다.
unconstrained/constrained optimization 에 대해 알아보는데 우선 unconstrained optimization은 말 그대로 목적함수만 있고 어떠한 제약이 없는 경우를 말하며, constrained optimization은 목적함수가 있는데, 어떤 제약이 가지고 목적함수의 최적화문제를 푸는 것을 배운다.
아래의 그림에서 4차 polynomial 함수를 볼 수 있다. 변수는 $x$하나가 있고 함수값은 $y$라고 해보자. 이 식을 목적함수라고 하면, 이 함수 값을 가장 작게하는 $x$값을 찾는 것으로 정의를 해볼 수 있다.
그렇다면 가장 작은 값을 가지는 부분은 아래의 파란색 선이 나타내는 -4.5 지역이 되겠다. 여기서 최소의 함수값을 주는 $x$값을 global minimum이라고 한다. 이 때 목적함수 값은 -47이 된다. 이 함수는 'smooth'하기 때에 경사를 생각해볼 수 있다. 그렇기 때문에 함수의 경사(gradient)를 활용함으로써 어디로 가야 할지 방향을 알아낼 수 있다. 아래의 그림에서는 까만색 화살표 방향으로 나아간다고 생각하면 된다.
하지만 만약에 오른쪽 부분에 움푹파인 곳을 보면 또 gradient가 0이 되는 부분을 볼 수 있는데, 이 부분을 stationary points라하며, 이러한 부분을 local minimum 이라고 한다.

위의 목적함수를 미분하여 gradient를 구하는 식은 아래와 같다.

(7.2)식이 0이 되게하는 $x$값을 구하게 된다. 이 예제에서는 $x$는 3개의 gradient값을 가질 수 있는데 즉, 3개의 stationary points를 가질 수 있는데, 이 포인트 중에서 어떤 애는 minumum, 어떤애는 maximum이 될 수 있다. 이를 알기 위해서 한번더 gradient를 구한다. (7.3)처럼 한번더 미분하여 gradient값을 구했을 때, 만약 양수이면 minimum이 되고, 음수이면 maximum이 된다.
gradient를 두번 미분했으니까 기울기의 변화를 의미하게 된다. 양수가 나온다는 것은 기울기들이 gradient 가 0인 지점을 지나면서 음의 기울기를 갖기 때문이고, 음수가 나온다는 것은 반대로 기울기들이 gradient 가 0인 또 어떤 지점을 지날 때 양의 기울기를 갖기 때문에, 빼 나가기 때문에 음수가 나온다고 할 수 있다.

일반적으로는 위의 예제처럼 쉽게 anlytic solution을 구하기 힘들다. 그렇기 때문에 어떤 특정 지점에서 출발하여 gradient를 구해나가는 방법을 사용한다. 다음 포인트로 이동할 때 얼마나 이동할 것인가를 구하는게 step size 라고 한다. 또한 어디서 시작하느냐도 상당히 중요한 결정 요소이다. 왜냐? local minimum에 빠질 수 있기 때문이다.
$f$가 미분가능 하고, 앞의 예제 처럼 analytic하게 솔루션을 구하기 힘들 때의 최적화 방법을 gradient descent 알고리즘이라 한다.

gradient descent는 주어진 함수를 한번 미분한 거라서 first-order optimazation algorithm이라 한다. second도 있다.
gradient descent는 초깃값에서 부터 gradient를 구하고 negative gradient방향으로 step size만큼 이동하면 된다. gradient는 현재 지점에서 함수값을 가장 가파르게 증가시키는 방향이다. 이 방향을 직관적으로 이해할 수 있다. 이 방향은 함수의 contour lines에 orthogonal 하는 방향이다. 이를 증명하면 내적으로 표현하여 나타낸다. 아래와 같이 contour lines에 대한 임의의 점 $P$를 둔다고 가정하면, $r(t)$라는 parametic equation을 활용해 최종적으로 $P$지점에서의 gradient와 $P$지점에서의 해당되는 contour line 접선의 방향을 나타냄으로써 그 방향에 orthogonal하다는 것을 알 수 있다.


즉 임의의 $P$에 직교인 방향(가장 가파른 변화)으로 나아가면 최종적으로 가운데 주황색점인 minimum을 향해 간다는 소리이다.
어떻게 궁극적으로 local한 minimum에 도달할 수 있는가를 간단하게 알아보면, 함수 $f(x)$라는 표면에서 $x_{0}$라는 지점에서 공을 굴린다고 가정하면, 가파른 경사를 따라 내려갈 것이다. 이는 곧 그 지점에서 gradient 값의 negative인 방향이다.

(7.5)는 하이퍼 파라미터인 step size 감마를 가중치로하여 이동한 만큼의 지점인 $x_{1}$을 나타낸다. 이를 일반적인 식으로 나타낸 것이 (7.6) 이다.

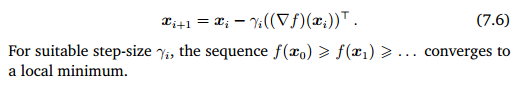
예제를 하나 살펴보자. 이차원 공간에 quadratic function(2차함수) 이 있다고 가정하자(7.7).

(7.7)을 미분하면 (7.8)의 결과.

미분을 하여 gradient 정보를 찾고 기울기에 negative한 방향으로 정한 step size만큼 이동하면서 local minimum에 접근해나간다. 연두색 박스 안에 처럼 minimum에 가까워질수록 움직임의 정도가 작아지는데, local minimum에 수렴하는 속도가 느려질 수 있다는 단점을 보여준다. 이를 보완하는 다양한 알고리즘들이 많이 나와있다.

위에서 말하던 step size는 직접 지정해주어야 한다. 이를 다른 말로 learning rate라고도 한다.
매 순간 step size를 변화시켜주는 Adaptive gradient methods 같은 것이 있다. 휴리스틱한 방법으로는 함수값이 증가하면 다시 돌아와서 step size를 줄여주고 반대로 함수값이 감소하면 돌아와서 step size를 높여주는 방법이 있다.
어느방향으로 가야 가장 가파르게 이동할 수 있는지, 속도 개념을 도입한 것이 바로 Gradient descent with momentum 이다. 과거 이력을 사용한다라고 생각하면 된다. 아래의 식(7.11)만 보아도 기존의 변화된 지점을 나타낼 때 $\alpha$ 붙은 term을 사용하여 새로운 지점을 결정한다. 전에 지점에서의 gradient 정보도 활용한다.

즉 지그재그 방향 말고 minimum쪽으로 가는 분홍색 화살표처럼 그 방향도 같이 고려를 해서 minimum으로 가는 다음 지점을 보다 신속하게 이동할 수 있게 된다.

계산적인 면에서 적은 연산량을 위한 방법인 Stochastic gradient descent가 있다.
머신러닝에서 목적함수는 보통 데이터의 loss의 합으로 나타나 이를 최소화하는 방법으로 나타나는데(7.13), 이 개별 loss는 또 미분가능하다. 이를 염두에 두고 살펴보자.

일반적인 gradient descent를 'batch' optimization method라 한다면

업데이트할 때 gradient 정보를 이용하는데, 여기서 loss를 미분한 것에 대한 합을 사용하게 되는데 데이터 size인 $N$이 만약에 엄청 나게 크다면 한 번 업데이트할 때마다 다 계산해서 합을 구해줘야하는데 시간이 너무 오래 걸리니까 $N$ 의 subset을 랜덤으로 $k$개 선택해서 계산한다고 하는게 mini-batch gradient descent 라고 한다.

$k$를 줄이면 계산량도 줄지만 noise가 증가한다. noise가 증가해서 bad local minimum을 지나침으로써 피할 수도 있다..
noise가 있더라도 좀 더 자주 파라미터를 업데이트하자. 고 시작한거지만 이제는 위 설명처럼 로컬 미니멈을 잘 피할 수 있다는 것이 또 이론적으로도 많이 증명이 되었다.
목적함수를 최소화하는 최적화 방법에 대해 알아보았고, 이밖에도 참 많은 방법들이 사용되고 있으니 적재적소에 좋은 알고리즘을 가져다 사용하자.
'수학' 카테고리의 다른 글
| Gram-schmidt Orthogonalization (1) | 2020.08.14 |
|---|---|
| Constrained optimization (1) | 2020.06.09 |
| Gaussian distribution (0) | 2020.06.03 |
| Singular Decomposition(2) (0) | 2020.05.30 |
| Singulardecomposition (0) | 2020.05.30 |




댓글