이번 장에서는 nonparametric method 중 unsupervised method에 해당하는 density estimation 하는 방법과 nonparametric하게 regression 하는 방법을 알아본다.
- 1. Unsupervised: Density Estimation
Density estimation 이라는 것은 말그대로 분포를 추정하는 것이다. Parametric method는 기본적으로 특정 확률분포함수를 가정을 하고 관측치들을 기반으로 추정을 한다. 예를 들면 정규 분포의 평균과 분산을 알고 있으니 어떤 값에 대한 확률밀도 값을 얻을 수 있다.
Nonparametric의 경우는 주어진 어떤 값들을 가지고 그 자체만으로 확률밀도를 추정하는 것을 말한다. 샘플들이 확률 분포 함수의 모양을 결정한다.
아래의 그림처럼 히스토그램으로 분포를 표현하고 확률밀도함수를 구성해 표현하기도 한다. 히스토그램 같은경우에는 rough한 표현처럼 보인다.
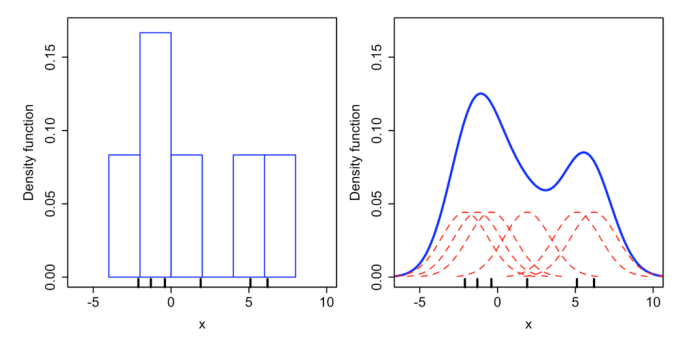
히스토그램의 rough한 표현을 좀 더 유연하게 표현해주기 위한 방법 중 하나는 Parzen-Window Density Estimation 이다.
Parzen-Window Density Estimation 는 아래의 그림 처럼 특정 영역을 window size에 따라 설정하여 그 영역에 포함된 관측치들의 개수에 비례해서 확률밀도를 계산하는 것이다.

특정 영역이라는 것을 정의해주기 위해서 window function 을 수식으로 표현해주어야 한다. window function 은 kernel function 이라고도 불린다. kernel density estimation이라고도 한다.
아래에 정의된 function은 $u$라는 벡터를 1부터 $p$ 개의 차원이 있을 때, 모든 차원의 값이 1/2 보다 작거나 같으면 이 함수의 값은 1이되고 아니면 0의 값이 된다는걸 의미한다. 소위 말해 관측값이 window 범위 내에 존재 하냐 안하냐를 결정해주는 함수라고 할 수 있다.

$x$라는 지점에서의 확률은 $p(x) \approx \frac{k_{n}/n}{V}$ 와 같다.

$x$ 에서의 밀도를 추정하기 위해서 $x$의 region의 중앙으로 잡고, region안에 포함된 샘플들의 개수를 세는 것이다.
$V$는 부피(volumn of the region)를 말하고, $k_{n}$은 Volumn안에 들어와 있는 관찰한 데이터 개수를 말하며, $n$은 일종의 normalize를 위해서 전체 개수$n$(observed data 수)를 $k_{n}$에 나누어 준다.
아래의 그림은 3차원의 영역을 보여주고 있으며, 빨간 점들은 Volumn내의 center에 위치한 $x$값을 기준으로 hypercube region안에 들어 있는 데이터를 나타낸다.

hypercube내에 존재하는 데이터 샘플들의 수는 $k_{n}$이며 수학적으로 표현하면 아래와 같이 나타낸다. 원래 $\phi$안에 $u$라고 표기되어 있었는데, $\frac{x - x_{i}}{h}$로 바뀐 것을 볼 수 있다. $x$는 밀도를 구하고자하는 지점을 말하고, $x_{i}$는 관찰한 데이터를 말한다.
이 식은 곧 영역 안에 들어와있는 데이터의 개수를 세는 것이다.

아래의 그림과 같은 예를 들어 $\phi(\frac{x - x_{i}}{h})$ 를 구해보자. $x$값들을 보면 2차원인 것을 알 수 있다. 먼저 $\phi(\frac{x-x_{1}}{h})$는 $\frac{0-0.25}{1}=1/4$, $\frac{0-0.25}{1}=1/4$ 로 x,y축에 대해 모두 1/2 보다 작은 것을 알 수 있고, 이는 boundary내에 위치해 있다는 것을 의미하게 된다.
$\phi(\frac{x-x_{3}}{h})$ 을 계산해보면, $\frac{0-0.7}{1}=7/10$, $\frac{0+0.4}{1}=2/5$ 로 1/2보다 큰 결과가 등장하여 이미 조건에 의해 범위 안에 없다는 0을 출력하게 된다.
boundary를 넓히고 싶으면 $h$의 값을 변경해주면 된다. 그림에서 보면 $h$를 2로 늘렸을 때, $x_{3}$이 범위내에 들어오게 되는 것을 알 수 있다.

window function을 토대로, Parzen-window estimation은 다음과 같은 형태를 갖는다. 위에서 $p(x)$를 $n$개의 데이터에 대해서 일반화시킨 식이다. $p(x)$에서 $1/n$은 그대로 나왔고, $k_{n}$도 그대로 있고, $V$부분만 hypercube의 Volumn으로 표현된 것을 알 수 있다.

$p_{n}$이 밀도함수인지를 체크한다. 먼저 확률이 음수 값을 가질수 없다는 점. 두번째, 모든 확률밀도들의 합이 1이 된다는 점을 토대로 보아, $p_{n}$은 밀도함수라고 할 수 있게 된다.

아래의 그림은 1차원에서 데이터 샘플 $D = \left \{ 2,3,4,8,10,11,12 \right \}$ 가 있다고 했을 때, $h$를 달리 하였을 때, 이 데이터들의 밀도를 카운팅한 그래프이다.
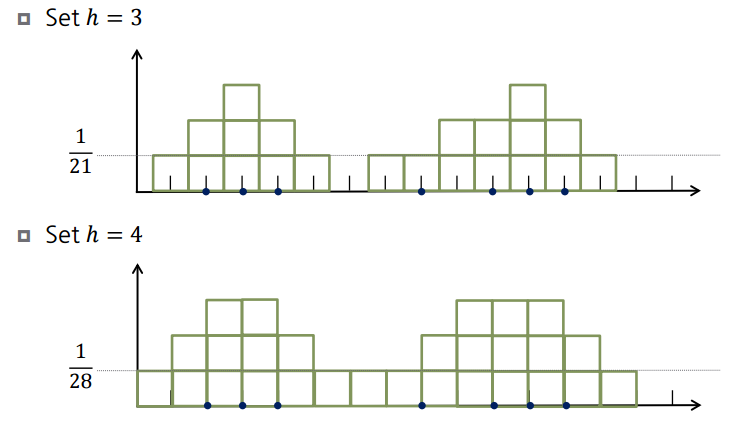
$h$가 3일 때, 데이터 3 과 같은 경우에는 좌우로 1.5, 1.5 안에 2와 4를 포함하여 총 3개가 되기 때문에 3의 값을 가지게 된다.
위의 그래프처럼 나타내면 좀 딱딱한 모습인 것을 볼 수 있는데, 다양한 window function을 사용해서 지금까지 영역에 들어오면 1 아니면 0인 식으로 딱딱하게 나누는 것말고 부드러운 density estimation을 할 수 있게 된다.
가장 유명한 window function 중 하나가 표준정규분포(standard normal distribution)이다. 평균이 0이고 분산이 1인 $N(0,1)$ 분포이다.

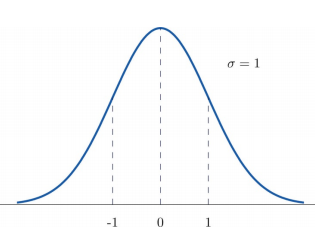
표준정규분포를 쓴다는 것은 $x$를 기준으로 표준정규분포를 그렸을 때, $x_{i}$들을 넣었을 때, 밀도값을 계산해보면, 평균에서 멀어지면 멀어질수록 낮은 밀도값을 갖게 된다. 앞에 카운트를 통해 그린 그래프는 영역에 포함된 샘플이 없으면 0의 값을 갖게 되는데, 이 정규분포의 경우에는 전체 실수에 대해 밀도값이 정의되어 있어서, 어디서 샘플을 관찰했던지 간에 많이 벗어나서 0에 가까울지언정 0의 값을 갖진 않게 된다.
아래의 그래프는 각 포인트별로 정규분포를 그리고, 각 정규분포 그래프마다 포인트($D$)에 해당하는 밀도값들을 다 더한 값들을 모으면, 빨간색 선으로 표시된 분포 그래프를 가지게 된다.
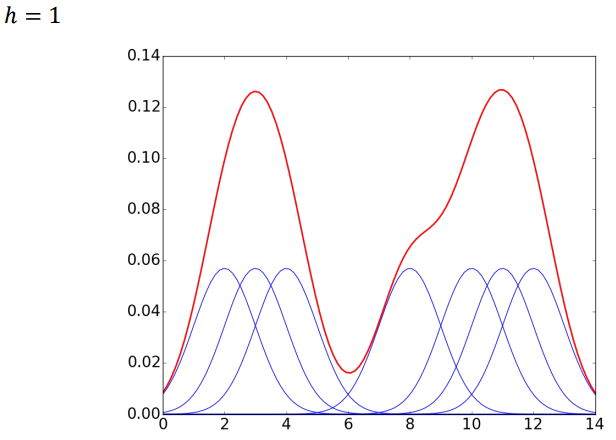
$h$는 분산과 같은 역할을 해서 $h$를 줄이면 분산이 줄어들게 되고, $h$를 늘리면 분산이 늘어나게 된다. $h$를 어떻게 정의하느냐에 따라서 데이터를 잘 설명할 수도 있고 아닐수도 있게 된다.

아래의 window function은 kernel function이 가져야할 조건을 만족하는 function 들이다. Exponential같은 경우는 전체 실수에 대한 고려를 하지만, 이 외에 if문을 통해 경계를 주는 경우에는 데이터가 영역에 있는 것에 대해서만 정의가 되고 아닌 경우에는 0을 주는 식으로 function이 설계되어 있다.

Bandwidth Selection
적절한 $h$를 찾는 방법으로 간단한 장점을 가진 방법이다. 추정된 표준편차값을 사용하며, 좀 더 robust하게 $h$를 찾기 위해서 A 와 같은 방법으로, 표준편차와 IQR값 중 더 작은 값을 사용하기도 한다.

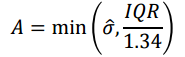
cross-validation을 통해서 $h$를 찾는 방법들을 사용한다. ISE(intergrated squared error)는 실제로 예측한 density estimation function과 실제값과의 오차 제곱을 적분한다. 아래 식에서 박스안에서 왼쪽에 해당하는 부분은 $h$를 넣고 하면 바로 구할 수 있는 부분이지만, 그 오른쪽의 부분에는 실제값이 들어가있다. 우리는 실젯값을 모르고 있는 상태이다. 그래서 그 값을 무엇으로 추정해서 쓸거냐에 따라서 다양한 방법이 있다.

그 방법들중 하나가, 아래의 방법이다. 자기 자신을 빼고 난 후에 밀도 추정을 하고 function을 만든 다음에 나온 값을 가지고 계산을 해서 위의 박스에 계산을 수행한다. 그래서 가장 error값이 작은 $h$를 찾게 된다.

multivariate case에서는 아래의 수식을 가지고 density estimation을 하게 되면 모든 axis에 대해서 동일한 $h$만을 사용하게 되는 문제가 발생한다. axis별로 scale이 많이 다르거나 분포가 많이 퍼져있거나, corelation이 있거나 하면 추정이 잘 안될 수 있다.

이러한 문제를 해결하기 위한 방법들 중에 첫번째, axis별로 scaling을 진행해주는 방법이 있다. 두번째, 데이터들을 covariance가 identity matrix가 되도록 transformation시켜주는 방법이 있다. 쉽게 말해 어떤 좌표를 다른 좌표로 옮겨서 추정하고 다시 가져오는 방법이 있다. 그러면 corelation을 없앨 수 있게 된다. 또다른 방법은 product kernel을 사용한다. 이 방법은 아래의 수식과 같은데, 1차원에 정의된 kernel들의 곱으로 multivariate의 kernel을 정의하는 것이다. 여기서는 축별로 서로다른 bandwidth를 사용한다.

- 2. Supervised: Regression
Nonparametric Regression의 경우에는 가지고 있는 sample 자체를 가지고 output을 예측을 한다. 대표적으로 kNN방법이 있다. 아래는 이웃들의 평균을 이용한 추정을 보여주는 kNN 식이다.

weight를 이용해서 jagged(들쭉날쭉한) 하다는 한계를 갖는다. 이말은 특정 데이터 주변 이웃의 y값의 평균을 활용하기 때문에 구성이 바뀔 때마다 다른 값을 가지게 된다.

이러한 문제를 해결하기 위해서 사용하는 것이 Kernel Smoothing이다. $w$ 들을 kernel function을 이용해서 구한다. density estimation처럼 normalize가 되어 있어야 weight들을 곱해서 다 더했을 때, 전체 weight들이 1이 되도록 맞춰줄 수 있다. Gaussian kernel을 이용하게 되면 특정 데이터 $x$와 가까이에 있는 데이터에게 weight를 더 많이 주게 되고, 멀어질수록 weight가 낮아지게 된다. Gaussian kernel같은 경우에는 모든 값들에 대해서 평균을 구할 수 있게 된다.


Epanechnikov kernel같은 경우에는 특정 범위를 벗어나는 순간 가중치를 주지 않게 되는 형태를 띈다. 그렇기 때문에 범위내에 있는 값들에 대해서만 평균을 구하게 된다.
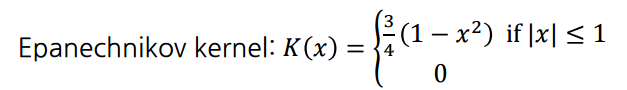

Kernel regression estimator(also called as Nadaraya-Watson kernel regression)이 아래의 수식이다. 즉, 커널 함수를 활용에 해당 weight를 준다는 것을 알 수 있다. 결국 $x$가 $x_{i}$에 가까울 수록 weight $y_{i}$는 더 큰 값을 주게 된다.

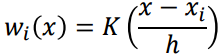
$x$에 대해 neighbor의 구성이 같다 할지라도, 그 거리에 따라 weight를 주어 모든 데이터에 대해 전부 다 다른 값으로 예측을 할 수 있게 된다는 장점이 있다.
아래의 그림은 nearest-neighbor와 kernel smoothing을 비교하고 있다. 파란색 선은 x,y 축 사이의 관계를 나타내고, 동그라미들이 observed value이다. 연두색 선은 예측된 y값들을 나타내고 있다. 빨간색 점에서 neighbor의 범위를 나타내고 있다. 노란색 점은 $w_{i}$라고 생각하면 된다.
왼쪽그림은 범위내에 들어오면 weight가 전부 동일하게 적용이 되는 반면에 kernel smoothing을 이용하여, 빨간점을 기준으로 거리에 따라 각각 다른 weight를 주게 된다.
왼쪽 그림에서 연두색선에는 $x$값이 변해도 $y$값이 같은 부분들을 관찰할 수 있다.
오른쪽 그림의 양쪽 끝에 빨간 원으로 표시된 부분은 양측에 대한 데이터를 전부 고려할 수 없기 때문에 오차가 더 커져버리게 되는 것을 말한다. 즉 input의 $x$값의 boundary에 bias가 발생하게 된다. 한쪽 영역에서만 봤기 때문.
이러한 문제를 해결하기 위한 것이 Local Linear Regression 이다.

Local polynnomial 은 Local Linear Regression의 일반화 버젼이라고 생각하면 된다. 즉 구역별로 회귀식이 들어간다고 생각하면 된다. 여기서 $\theta$는 Local polynomial로 추정된 값이다. 그리하여 $x$에 대해 아래의 식을 최소화하는 추정을 한다.

만약에 Linear를 쓴다면 $\theta$ 가 아래처럼 베타들로 구성된 식을 사용하여 SSE를 최소화하는 작업을 할 수 있다.

아래의 식은 SSE(sum of squared error)를 나타내는데 보이지는 않지만 weight 가 전부 1이라고 할 수 있다. 즉 위의 식에서 오차를 나타내는 term앞에 $K(\frac{x-x_{i}}{h})$가 1인 것이다.

Linear regression 과 같은 방식을 적용하는데, 예측하고자 하는 $x$가 주어지면 weight를 다 구한다음에 전체적으로 minimize하게 되어 최종적으로 $\beta$값을 추정하게 된다. 그렇게 되면 좌표마다 각각 다른 $\beta$값을 가지게 된다. 그것이 일반적인 Linear regression과의 가장 큰 차이점이라고 할 수 있다.

$x$에 local linear regression을 Matrix fomulation으로 나타내면 아래와 같다. 차이점을 보면 $\Omega$ 로 나타난 행렬은 weight에 해당하는 kernel function 값에 해당하는 diagonal matrix가 있다. 해당하는 $x$들이 대해 각기 다른 weight들을 담고 있다.
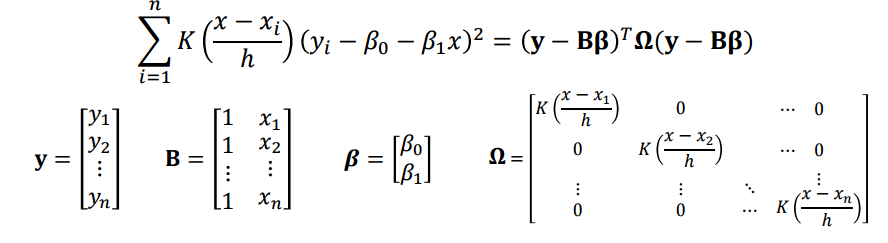
일반적인 regression에서는 $(y-X \beta)^{T}(y-X \beta)$를 $\beta$에 대해 미분해서 0이 되게 최소화하는 방식으로 아래와 같이 최종적으로 베타를 추정한 식을 구하게 된다.

그리하여 특정 $x$에 대해 가장 best $\beta$라고 하는 것은 사이에 diagonal weight matrix를 넣어주기면 하면 된다. 그리고 최종적으로 $y$예측치를 구할 수 있다.

여기서 $\vec{x} = [1 \ x]^{T}$ 이다. 아래의 추정치는 Local Linear Regression 방식으로 $y$ 추정치를 얻은 것이다.

아래의 그림은 Nadaraya Watson kernel function을 적용한 것과 Local Linear Regression을 가지고 각각 추정한 그래프를 나타낸다. 둘 다 동일한 Kernel function을 사용하여 $x$에 대한 window가 동일하다.
local linear regression은 local한 영역에서 linear하다고 판단되면 사용하면 되고, 고차원의 function으로 fitting을 해야한다면, local polynomial function을 사용하면 된다.
Local Linear Regression의 그래프는 보시다시피 local 영역에서 linear한 분포를 보이기 때문에 weight도 그렇게 적용되어 보다 bais를 줄일 수 있게 된다. boundary effect가 좀 완화된 것을 알 수 있다.

'머신러닝' 카테고리의 다른 글
| regression (0) | 2020.10.17 |
|---|---|
| Clustering (0) | 2020.10.17 |
| 회귀분석 with python (0) | 2020.03.21 |
| randomforest for regression (2) | 2020.03.06 |
| 엔트로피(Entropy) (0) | 2020.01.06 |



댓글