이번 장에서는 graphical model 에 대해 알아본다.
자료들을 확률적으로 모델링하는 방법 중에 하나이다. 제대로 공부를 하려면 한학기 내내 공부를 해도 부족할 정도로 양이 많다. 여기서는 간략한 개념정도만 학습한다.
확률모델인만큼, 각각의 변수들을 일종의 노드로 생각을 하고, 변수와 변수 사이의 관계를 엣지로 표현한다.

Undirected Graph: 서로 인과, 선후관계는 모르고 관계를 맺고 있고 방향이 없는 그래프.
Factor Graph: 연결 사이에 어떤 요소가 존재하는 그래프.
Bayesian Network: 방향성이 있는 것이 Directed이고 거기에 방향이 있지만 acyclic(화살표를 따라서 자기자신으로 돌아오지 않는) 형태의 그래프.
아래의 그림은 A가 B에 영향을 주는 경우. 이 둘은 더이상 독립이 아니기 때문에 이 둘의 결합확률은 두 확률의 곱으로 표현이 안되는 것이고, 독립이 아니기 때문에 B의 조건부확률에서 독립이라는 가정하에 B의 확률과 같다고 정의를 할 수 없다.


그래프는 가진 데이터에 대한 확률 분포를 얻고자 한다.
먼저 Baysian Network 에 대해 알아본다.
- 방향이 있고, acyclic한 그래프.
아래의 그림을 예로 들면 A,B,C의 join probability를 구하는 것(어떻게 쪼개서.)이 목적이다.
변수가 많아지면 추정할게 많아지고 분포가 어려워 진다. 그래서 변수 사이의 관계를 알아서 이를 바탕으로 결합확률을 여러개의 확률분포로 쪼개개 된다. 그래서 쪼개면서 더 단순하게 만들고 각각을 추정하는 것이 전체를 추정하는 것보다 쉬워지게 된다. 그리고 곱의 형태로 최종적으로 결합확률을 구하게 된다.
각 노드들 A,B,C에 대한 결합확률을 분해하여 표현이 가능하다.

모든 변수들 간의 결합확률을 구하는게 목표라 했다. 결합확률은 chain rule에 의해 조건부 확률로 쪼개서 여러개의 곱으로 표현이 되게 된다. 조건에는 여러가지 변수가 들어가지만 왼쪽 파트에는 딱 하나의 변수만 들어갈 수 있는 조건부 확률들의 곱으로 표현.

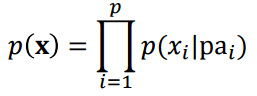

그래서 아무리 많은 변수들이라도 chain rule에 의해서 조건부확률 곱으로 쪼갤 수 있다.
위의 방법은 변수들이 서로 완벽하게 다 연결이 되어 있는 경우에를 말함. fully connected.
만약 변수들이 독립인 경우를 안다면, 간단하게 표현할 수 있게 된다. 만약 P(C|A,B)에서 C와 A가 독립이면, P(C|B)로 표현 가능하다는 것이다.
그래서 아래의 식처럼 $pa_{i}$는 부모노드를 말하며, 자신에서 화살표를 내린 노드를 말한다. 그러니까 화살표없고 독립인경우는 아예 포함을 시키지 않아도 되어 독립임을 안다면 계산에서 제외해도 되니 계산량이 준다.

아래의 그림을 보면, x1,2,3는 부모노드가 없으니 본인의 확률만 들어가게 되고, 나머지는 자신의 부모노드가 있는 경우를 조건에 넣은 조건부확률로 최종적인 결합확률을 표현한다. fully connected보다 훨씬 단순해진 것을 알 수 있다. 또 변수가 많아지면 제대로 추정하기가 힘들어진다.

베이지안 네트워크를 구성하는 방법.
1. fully connected graph를 생성한다.

2. 조건부 독립을 확인하고 위의 조건부확률로 쪼개진 결합확률의 계산을 단순화 한다.
이 때 단점이 존재한다. 변수들의 초기 순서에 의존하게 된다. 만약 순서가 꼬여 있으면, 이들의 관계를 찾는데 시간이 더 소요된다는 것이다. chain rule 적용 초기에 순서를 어떻게 정의하냐가 중요해진다.
예를 들어보자. 아래와 같이 데이터가 주어지고, 1번을 거쳐 2번으로 가는 것이다.

더 자세히 보면
1번 chain rule을 적용 하면,

2번 조건부독립을 찾아 단순화시켜주면,

최종적으로 다시 정리를 해주면, 다음과 같이 된다.
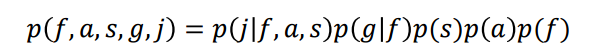
베이지안 네트워크를 구성할 때는 그래서 순서를 잘 정리해야 가장 단순한 베이지안 네트워크를 구성할 수 있다.
베이지안 네트워크를 얻어지면, 이 결합확률로 부터 확률분포를 얻을 수 있다.
이제 관측된 데이터를 가지고 베이지안 네트워크의 확률을 계산한다.
아래 수식에서 보면, 결합확률분포는 부모노드들에 영향을 받는 것들로 구성할 수 있고, 분포 모양을 뭔지 다 안다고 가정한다면, 관측치를 가지고 parameter들을 추정해야한다.
조건부 확률이 정규분포를 따른다고 하면, 해당하는 mean과 variance를 추정해야한다. 는 방식으로 진행하면 된다.

베이지안 네트워크에서 확률분포를 추정하는 문제는 최종적으로 $\theta$들에 대한 분포를 얻는 것이다. 우리가 parameter를 모를 때, 점추정이나 구간추정을 했었다. 여러가지 추정식이 존재하는데 이 문제에서는 $\theta$들에 대한 가장 좋은 추정치를 점추정할 수 있다.
베이지안 네트워크의 경우에는 parameter에서도 분포를 추정한다. 관찰한 데이터가 바뀌면 추정치도 바뀌고, theta도 확률분포로 보게 되기 때문이다.
위의 식에 posterior term에 의미는 $S$라는 우리가 앞서 구한 구조하에서 theta들의 posterior를 보게 되는 것이다.
이것은 베이즈 이론에 의해 prior, likelihood, evidence로 쪼개서 보게 된다. prior는 우리가 데이터나 구조를 모르고 있는 상태에서 prior의 theta들의 분포, parameter에 대한 분포를 prior라 한다. theta와 구조를 안다라고 했을 때 관찰한 데이터들에 대한 분포를 말하며 likelyhood라고 한다.
우리가 데이터 관찰 전에 theta들에 대한 분포인 것이다. 그리고 데이터를 관찰하고 나면 정보를 얻게 된것이고 그리고 각 theta에 대한 가능도들이 다 달라지게 된다.
다시, likelyhood라는 것은 우리가 어떤 분포를 가정했을 때, 그 분포 하에서 우리가 관찰한 데이터가 얼마나 봄직 한지를 얘기할 수 있다.

아래의 예시를 살펴보자.
문제는 fraud를 찾는 문제 였다. 모든 변수들이 카테고리 변수이다. 각각 카테고리의 확률이 나타나 있다. 확률의 합이 1 이므로 굳이 적지 않아도 되는 경우에 대해서는 존재하는 확률들을 1에서 빼면 나머지의 확률을 얻을 수 있다.
이 예에선 전부 카테고리 변수이기 때문에 각각의 조합에 대한 표를 만드는 것과 다르지 않다.

베이지안 네트워크를 상황에 따라 구분지어서 살펴보자.
먼저 Complete Data에 대해서는,
우리가 구조를 알고 있다면 바로 결합확률을 쉽게 분해할 수 있기 때문에 각 조건부확률분포에 theta를 추정하는 문제가 되는 것이다.
우리가 구조를 모른다면, 구조를 알아내는 작업을 해야한다. 가진 데이터를 가지고 이 데이터 구조를 잘 나타낼 구조를 찾는다. 그런다음에 분포를 추정하는 작업을 하게 된다.
하지만 데이터 중에 missing 값들이 있는 incomplete data라면, 그 data가 어떤 값이 였냐에 따라서 parameter들이 또 달라질테니 문제가 더 복잡해진다. 최적화 문제를 풀어야한다..

이번에는 구조를 어떻게 학습할까에 대해 가장 간단한 알고리즘인 Greedy Hill Climbing 에 대해 알아본다.
구조를 어떻게 학습할까라고 하는 것은 다양한 데이터들을 관찰하고 나면 이 데이터로 부터 가장 최적의 베이지안 네트워크 모양을 찾는 것이다.
크게 두가지로 나뉜다.
Constraint-based: 변수들을 분석해서 위 그림에 엣지들을 보면 부모노드들을 보고 엣지를 결정하고 구조를 만드는 과정.
Score-based: 있을 수 있는 모든 구조들을 모두 찾고, 데이터가 주어지면 그 구조와 얼마나 부합하는지 Scoring해서 가장 높은 score인 구조를 선택하는 과정. 변수 개수가 조금만 많아져도 가능한 구조들이 많아져서 시간이 많이 걸린다.
그래서 사용하는 방법이 Heuristic한 방법인데, search를 하는 규칙 같은 것이다. 다음 체크해야하는 순서들을 생성해내는 방법을 만들어 전부 다 뒤지지 않고, 더 좋아지지 않을 지점까지만 가서 멈추는 식으로 하는 방법이다.
이러한 방법이 바로 Greed 알고리즘이다. 각 단계에서 가장 좋은 search 할 것을 찾는 것을 방법이다. 조금씩 개선 시켜나가는 방법이다. 적어도 local optimum 에 도달하는 것을 보장해주는 방법. global에 대한 것은 보장x.
Greedy Hill Climbing은 기존의 구조에서 엣지를 제거하거나 추가하거나 방향을 바꾸면서 주변부의 구조를 정의하는 방식으로 진행한다. 그리고 이미 지정된 scoring function으로 점수를 매겨 더 좋은 점수인 구조로 옮긴다. 베이지안 네트워크에선 이 때 acyclic이 되도록 생성해야하는 제약이 있다.
1,2. 초기 구조 설정.
3. 엣지 제거, 추가, 방향변경 등으로 구조를 변경.
4. score를 따라 구조를 다시 set.
5. 더 나은 구조를 찾지 못할 때 까지 반복

새로운 구조를 찾는 예시는 아래와 같다.
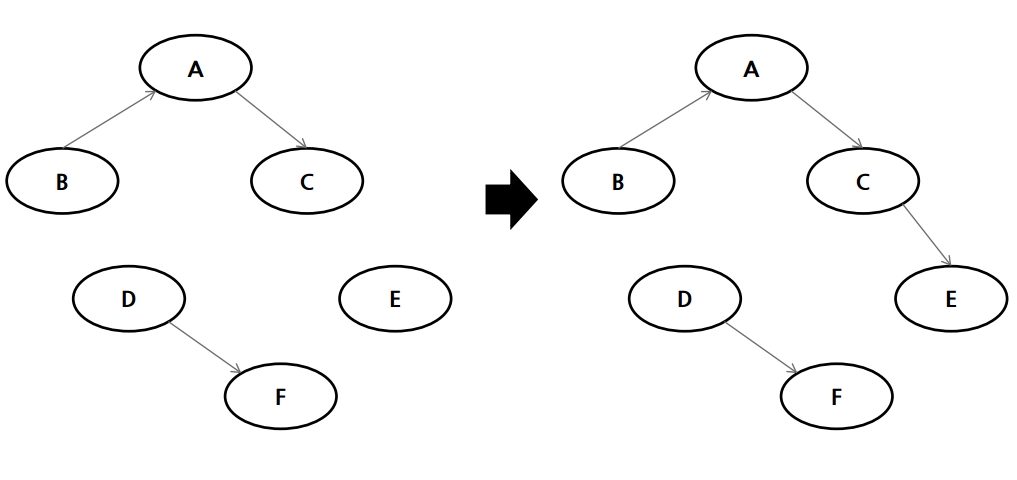


Scoring function
지정된 구조에 대한 likelyhood의 값에서 구조의 복잡도를 데이터 개수 가중치를 곱한 것을 빼줌으로써 score를 결정한다.
이 데이터를 얼마나 봄직하냐만 봐도 되지만, 복잡도를 패널티로 주어 너무 복잡하면 점수를 낮추는 term을 주었다.
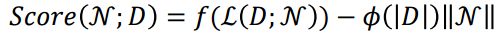

MDL(Minumum Description Length) 방법은 Cost로 하여 오히려 score가 낮을 수록 구조가 좋다고 판단할 수 있게 한다. |N|은 구조의 parameter의 개수이며 네트워크의 크기를 나타냄.


최종적으로 데이터 D와 N에 대한 네트워크의 log likelyhood는 아래와 같은 수식으로 표현된다.
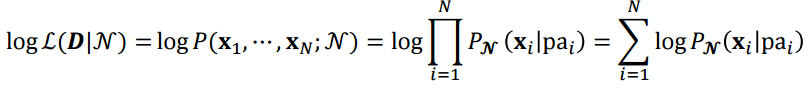
parameter를 어떻게 추정할지 예시를 통해 알아보자.
우선 Fraud와 Gas 변수에 대해서만 살펴보자.

fraud가 yes일 때의 gas의 parameter를 추정하고, no일 때도 마찬가지로 추정한다. 각각 fraud가 yes일 때, no일 때, 확률의 합은 각각 1 이다. 그래서 전체 추정할 parameter는 2개가 된다. 지금은 이진이라 하나의 카테고리에 대해서만 추정해도 나머지의 추정값을 알 수 있기 때문이다.

다음으로는 범주형 변수에 대해 log likelyhood의 값은 어떻게 되는지 알아보자.
$n$은 변수의 개수(노드의 개수)이고, $r_{i}$는 변수 $x_{i}$의 state 개수를 말한다. $q_{i}$는 $i$의 부모노드 개수이다.
$N_{ijk}$는 $j$번째 부모노드에 대한 $k$번째 state의 샘플들의 수를 말한다.
$\theta_{ijk}$는 $j$번째 부모 노드의 $k$번째 state의 parameter를 의미한다.

예시로 들어 위의 식을 적용해보면 아래와 같다.

주머니에서 흰공 7개와 파란공 3개를 뽑았다고 가정해보자. 그렇게 되면 likelyhood를 알 수 있다.
추정해야할 parameter인 파란 공에 대한 확률 p 흰공에 대한 확률을 1-p라고 하게 되면, 아래와 같은 수식으로 나타내게 되어 최종적인 log likelyhood를 구할 수 있다.
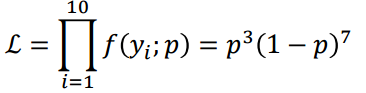

아래의 수식처럼 $N_{ij}$를 곱하고 나누는 트릭으로 하면 일종의 확률로 보이는 term을 만들 수 있게 된다.

이에 Gibb's inequality에 의해서 $\theta$ 값이 p(x)가 되면 그 값은 maximum이 되게 된다.

이제 이 네트워크 구조에 대해 score function 중 위에서 보았던 MDL에 넣어서 score를 계산하게 된다. (r - 1)은 나머지 하나의 category라 자동적으로 구해지므로 계산 과정에서 -1을 해주는 의미.

다시 term 별로 정리를 하면 log likelyhood 파트와 패널티가 들어가 가중치를 고려한 네트워크의 구조의 복잡도 파트로 나눠 볼 수 있다.

'머신러닝' 카테고리의 다른 글
| Nearest Neighbor Method (0) | 2020.10.18 |
|---|---|
| Support Vector Machine(1) (0) | 2020.10.18 |
| Naive Bayes Classifier (0) | 2020.10.18 |
| Ridge and Lasso Regression (0) | 2020.10.17 |
| regression (0) | 2020.10.17 |




댓글