Convolutional Neural Networks는 time-series data, image data, video data 와 같은 grid-like topology 형태에 잘 사용된다. (연속되어 있는 값들 사이의 관계가 데이터를 이해하는데 중요한 요소.)
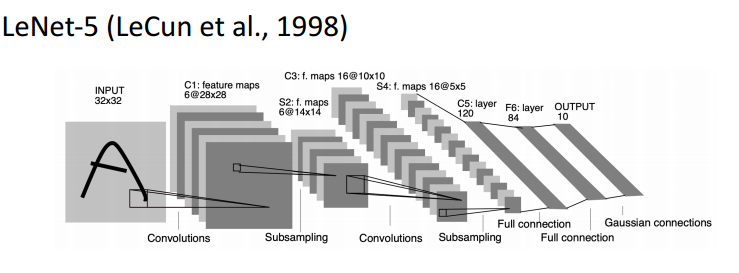
아래는 손글씨 글자 이미지를 분류하는 작업이다. 이전에 MNIST데이터와 유사한 데이터다.
input을 보면 32x32 인 2 dimension 데이터를 직접 사용한다. 가운데를 보면 convolutions라는 layer들이 쌓여있고, 후반부에 Full connection은 dense layer를 말한다. 즉 하나 이상의 Convolutional layer를 가지고 있으면 convolutional neural network가 된다.
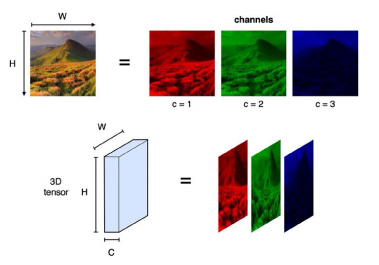
3D tensor는 3개의 축을 지닌 3-dimensional array이다. 대표적인 사례가 RGB color이다. 이미지 같은 경우에는 axis가 height,width, channel로 구성되어 있다. red,green,blue를 가지고 하나의 컬러를 표현하기 때문에 총 3개의 채널이 또다른 축으로 쌓여있는 형태를 가지고 있다. c=3이 된다. Grayscale image처럼 흑백인 경우에는 2D tensor라 할 수 있다.
아래는 color video를 나타낸다. 이는 4D tensor이며, height, width, channel 그리고 time 이라는 또다른 축으로 나열되어있다.

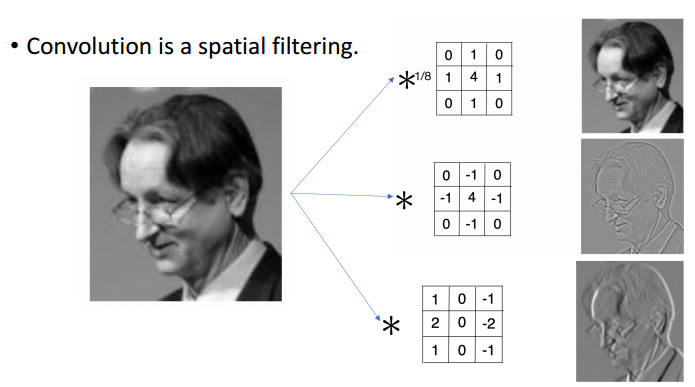
사진같은 이미지에 필터를 넣는 작업을 해보았을 것이다. Convolution은 data에 spatial하게 filtering을 해주는 것이라 생각하면 된다. 뉴럴 네트워크의 대가 제프리 힌턴(Geoffrey Everest Hinton)의 사진이다. 이 사진에 오른쪽에 있는 각기 다른 array를 입혀줌으로써(convolve) 다른 결과를 출력하게 된다. 두번째는 엣지효과, 세번째는 음각효과 같은 특징을 지녔다는 것을 유추해 볼 수 있다.
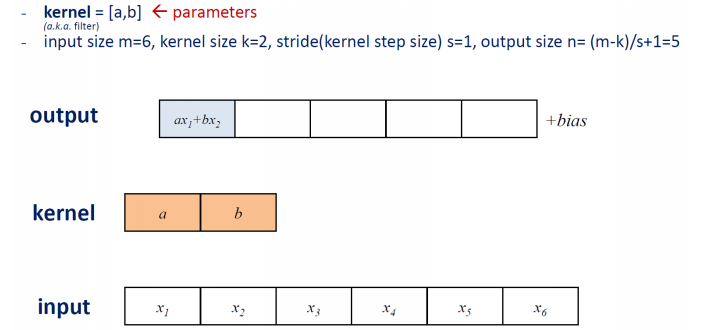
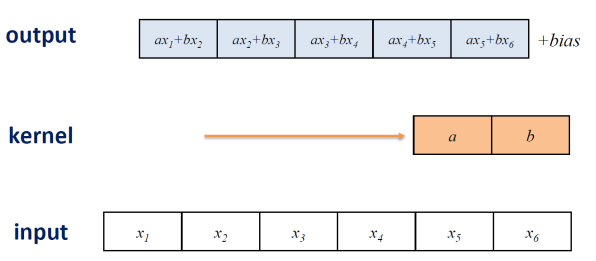
Convolution은 어떻게 연산이 진행될까, 1 Dimension Array input이 아래에 있다. 방금 말한 filter를 kernel이라고 부르기도 한다. kernel이 a,b라는 parameter일 때, input x이 1 dim으로 size가 6이다.
kernel이 두개의 parameter를 가지고 있기 때문에 kerner size = 2라고 한다. 앞선 네트워크에서 dense layer에서 모든 input노드들에 대해서 weighted sum을 진행했지만, kernel에서는 kernel size만큼의 input 노드들의 weighted sum을 한다.
컨볼루션에서 stride가 의미하는 것은 stride만큼 kernel이 input에 대해 sliding window방식으로 움직이는데 몇 칸씩 띄어가면서 움직일 건지를 말한다. output size와 같은 관계식을 통해서 output의 크기를 알 수 있다. m은 input의 크기, k는 kernel의 크기, s는 stride 크기를 말한다.
weighted sum을 모두 수행한 output은 아래의 그림처럼 출력된다. 출력된 output이 activation function을 만나서 변형이 되는 진행을 거치게 된다.
이처럼 kernel window가 stride만큼 sliding해가면서 대응되는 input을 weighted sum 하는 연산이 convolution라고 할 수 있다.
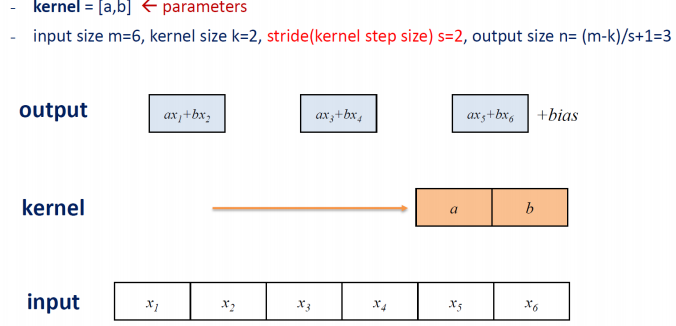
아래의 그림은 stride를 2로 주어서 kernel window 가 두 칸씩 움직이므로 output은 3개가 되게 된다. 이로써 우리는 stride를 조절해가면서 input에 대해 적은 크기의 output을 출력할 수 있다.
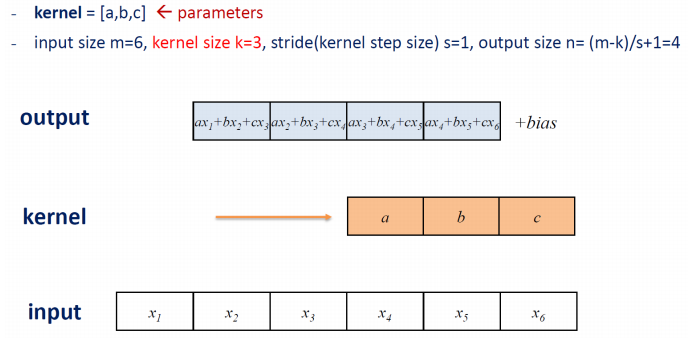
아래의 그림은 kernel size를 3으로 늘린 결과를 나타낸다.
위의 그림을 네트워크 그림으로 표현하면 아래의 그림과 같이 나타낼 수 있다. dense layer 처럼 full connection 과 차이가 있다는 것을 염두에 두자. dense layer의 경우에는 output 노드의 개수를 parameter로 주었다. 그럼 자동적으로 hidden node의 수와 input 들이 완전 연결을 가지게 된다. 하지만, convolution에서는 output 노드의 개수를 명시적으로 선언해주지 않는다. 그렇기 때문에 위 그림의 output size 처럼 kernel size, stride size에 따라서 결정이 된다. 이러한 차이점이 있다.
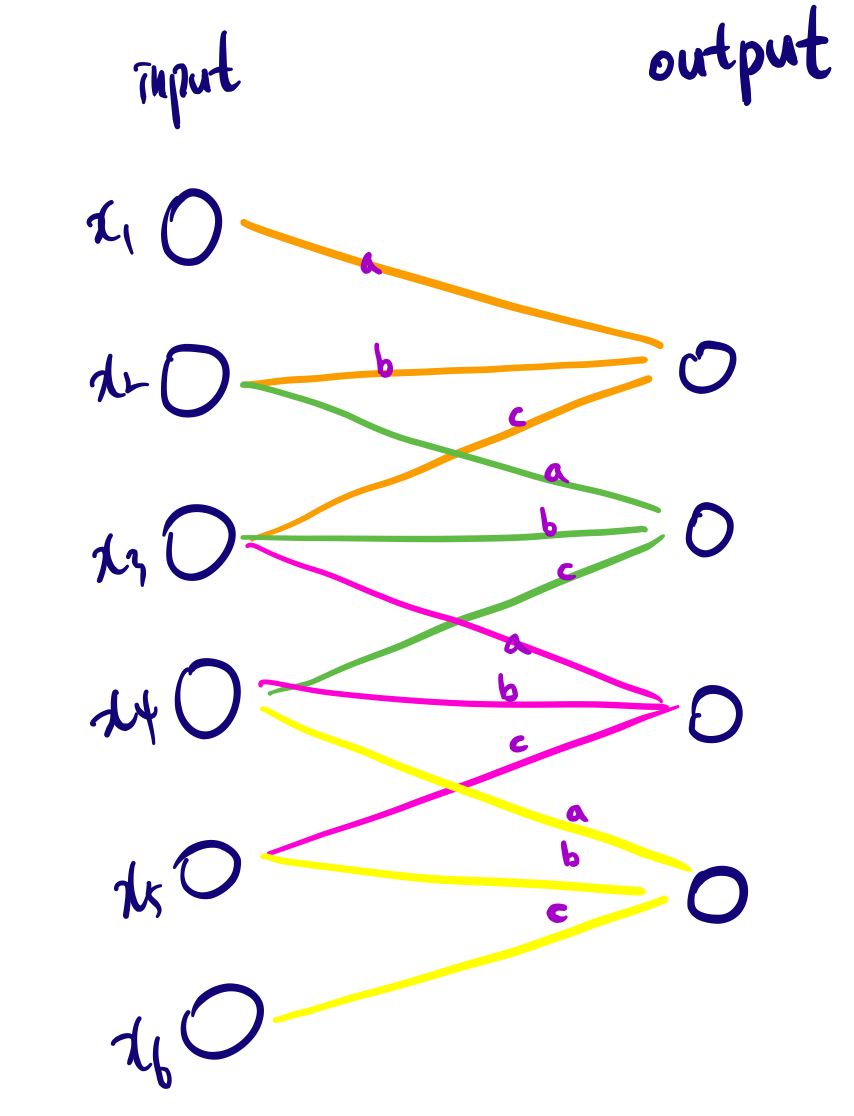
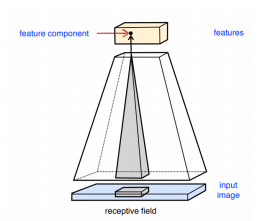
Receptive field라는 개념을 알아보자. 특정 output 노드를 계산하기 위해 필요한 input 영역의 크기라고 생각하면 된다. 바로 위 그림처럼 하나의 output 노드하나의 값을 계산하기 위해 연속된 3개의 input 노드가 필요했다. 이 때 output node의 receptive field size는 3이 된다.
output 노드들의 집합을 feature map이라고 부르는데, 이 특정 output노드의 값을 연산하기 위해서 오직 receptive field안에 들어오는 input들만 연산에 포함되게 한다.
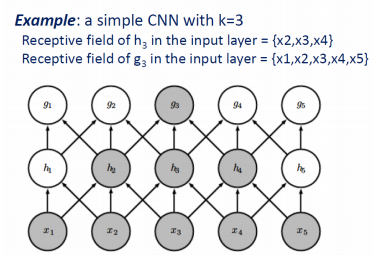
receptive field를 크게하고 싶으면 kernel size를 크게하거나 layer를 여러개 쌓는다. 아래의 경우 $h_{2}, h_{3}, h_{4}$는 각각 receptive field size가 3이다, 반면$g_{3}$는 $x_{1}, x_{2}, x_{3}, x_{4}, x_{5}$를 receptive field로 받아 size가 5가 된다.
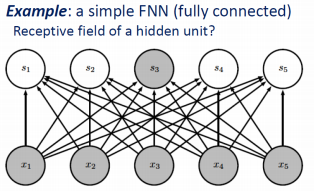
dense layer의 fully connected의 경우에는 아래의 그림처럼 각 output 노드의 receptive field size가 5가 될 것이다.
아래의 고양이 이미지가 100 x 150 이라 한다면,

컴퓨터는 아래의 숫자들(0-255의 값을 가진 8bit -> uint8)로 이뤄진 2D array로 인식한다.

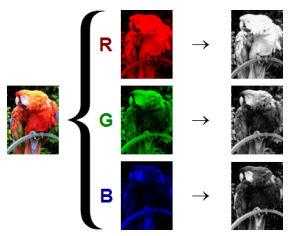
컬러이미지의 경우에는 red, green, blue 각각 2D array 가 겹겹히 쌓여있는 3D tensor로 인식하게 된다.
- 2D tensor(흑백이미지) convolution 하기
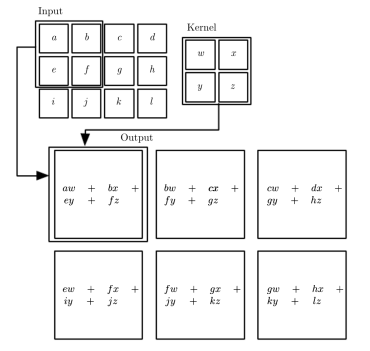
3 x 4 2D tensor를 2 x 2 array 형태의 kernel로 convolution 하면 sliding 해가면서 weighted sum을하여 output을 산출한다. 이 output node은 scalar값으로 모여서 결국 행렬로 나타나는 과정을 통해 3 x 4 행렬을 2 x 2 행렬로 convolution 한 일련의 과정을 알 수 있다.
여기서 학습을 통해서 결정해줘야 하는 parameter는 kernel에 존재하는 $w, x, y, z$라는 weight 이다. 여기서 학습을 통해서 결정할 수 없는, 학습 전에 결정해주어야 하는 hyperparameter는 kernel size, stride 값이 되겠다. 여기서는 kernel size = 2 x 2, stride = 1이 되겠다.
-3D tensor(컬러이미지) convolution 하기
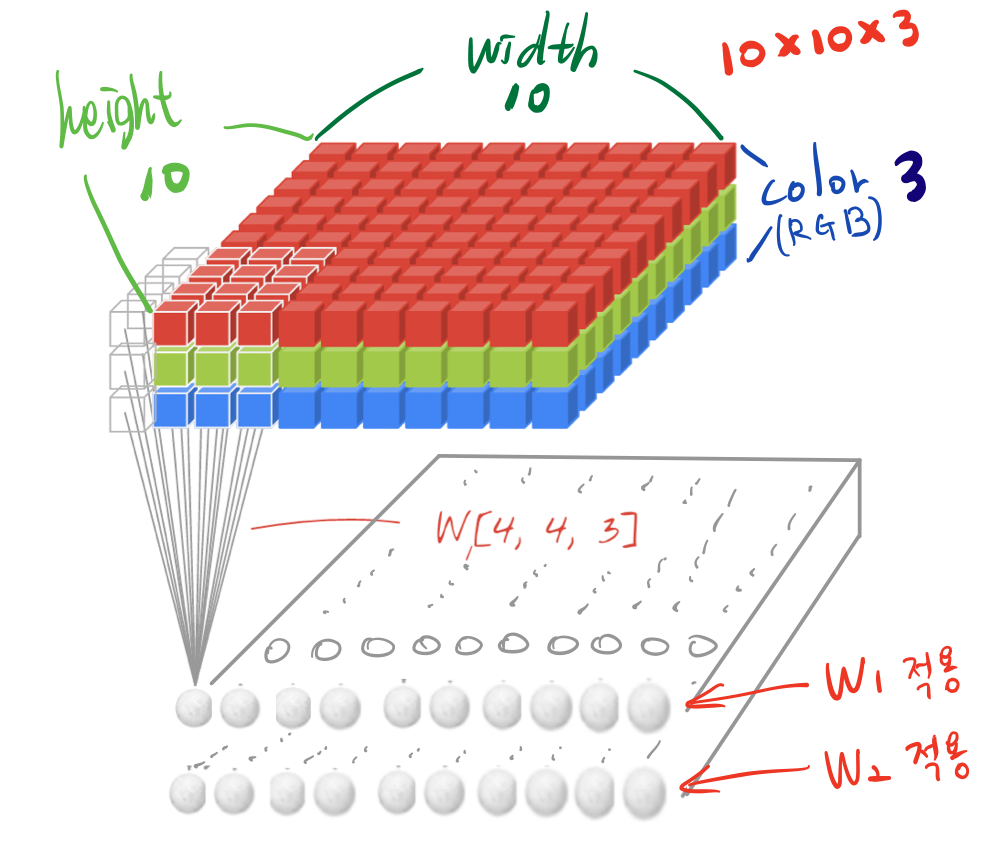
다음과 같은 데이터(10x10x3)를 convolution 한다고 해보자.
height와 width 이 2 Dim을 sliding 해가면서 weighted sum을 수행한다. 그러면 2D convolution이 되는 것이다. 만약 입력이 3D tensor가 입력된다 하더라고 커널이 1Dim 상에서만 sliding 하면 1D convolution이 되는 것이다.
kernel 과 filter의 차이를 분명히 해야한다. kernel이라는 것은 sliding window 하는 영역에서의 크기이다. 여기에서는 4x4이라고 할 수 있다. filter라는 것은 실제로 kernel이 weighted sum 하는 영역의 크기이다. 여기에서는 4x4x3이라고 할 수 있다.
4x4kernel에서 color 축으로 쌓인 모든 값들 즉 아래 그림을 토대로 4x4x3 cube모양을 eighted sum을 하여 스칼라 값을 산출해야한다. 즉, 이러한 weighted sum을 하기 위해서 4x4 kernel이 실제로는 4x4x3 이라는 weight를 가지고 있어야 된다. 엄밀히 말하면 kernel과 filter는 다른데 통상적으로 구분하지 않고 사용하게 된다.
filter의 크기가 weight의 개수인데, 여기서는 4x4x3 = 48개의 weight를 갖는다.
2D convolution이라고 부르는게 2D 입력을 받는게 아니라는걸 꼭 염두에 두자. 여기서 kernel이 sliding하는 dimension 크기를 말한다. 2 dimension에서 sliding하면 2D convolution이고, 3 dimension에서 sliding하면 3D convolution이라고 한다.
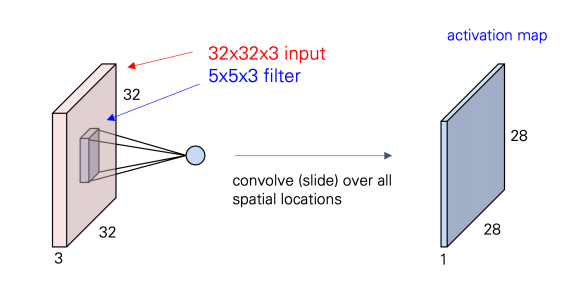
다른 그림을 통해 좀 더 자세하게 살펴보도록 하자.
input 이 32x32x3 인 3 dimension 이고, 5x5x3 인 75 개의 weight를 갖는 filter이다. filter를 거치면서 scarlar들이 output 으로 나오면서 28x28x1과 같은 array가 생성된다. 이 activation map(feature map)은 기존의 input에서 filter의 가중치 행렬과의 weighted sum을 한칸씩 slide해가면서 하기 때문에 padding이 없으니 28번 옆으로 이동하면서 weighted sum을 계산하고 그러다보면 오른쪽 결과와 같은 dimension을 가지는 output이 된다.
한번더 수행하게 되면 activation map은 28x28x2 가 된다. 이전의 map과의 차이는 convolution하는데 있어서 filter가 가지는 weight값이 다르다는 것이다. 다른 특징을 detect하는 filter를 가지고 그에 해당하는 activation map을 생성하는 것이다.
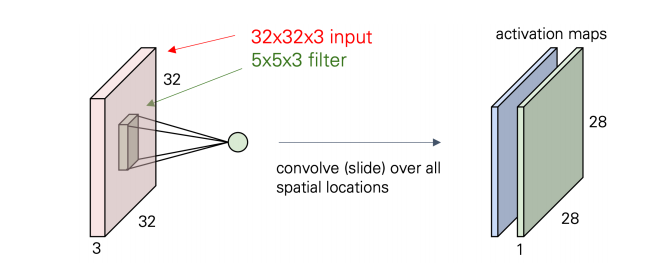
kernel size 가 5x5(x3) 로 convolution을 각기 다른 filter로 6번 수행하고 output을 쌓으면 activation map(feature map)이 된다.
생성된 activation maps는 그다음으로 convolution을 진행할 게 있다면 input으로 들어가게 된다. 다음 convolution도 5x5 kernel을 갖는다면 5x5x6 filter 를 가지고 convolution을 수행한 weighted sum들을 토대로 output을 생성하게 된다.
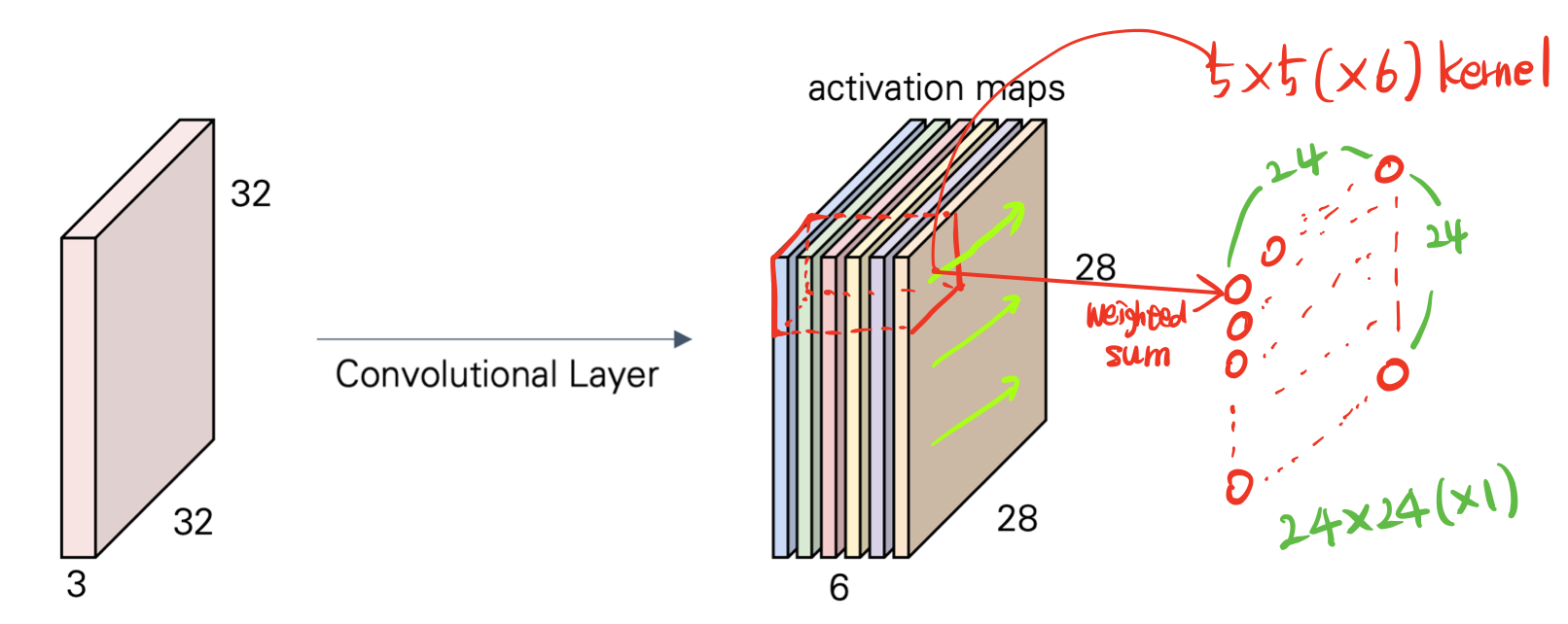
- activation maps의 size를 계산해보자.
아래는 서로다른 Filter가 2개 있고 각각 convolution을 하는 모형이다. output shape는 오른쪽의 공식에 따라 쉽게 구할 수 있다. padding에 대해서는 후에 다뤄 설명은 하지 않고, 여기서 padding은 0이므로 신경쓰지 않고 계산하면 6x6x3 input을 3x3x3 filter를 거쳐 4x4x1 activation map을 구하고 각각 map을 결합하면 최종적으로 activation map 4x4x2 가 된다. 여기서 4x4x2 에서 2는 filter의 개수를 나타낸다.
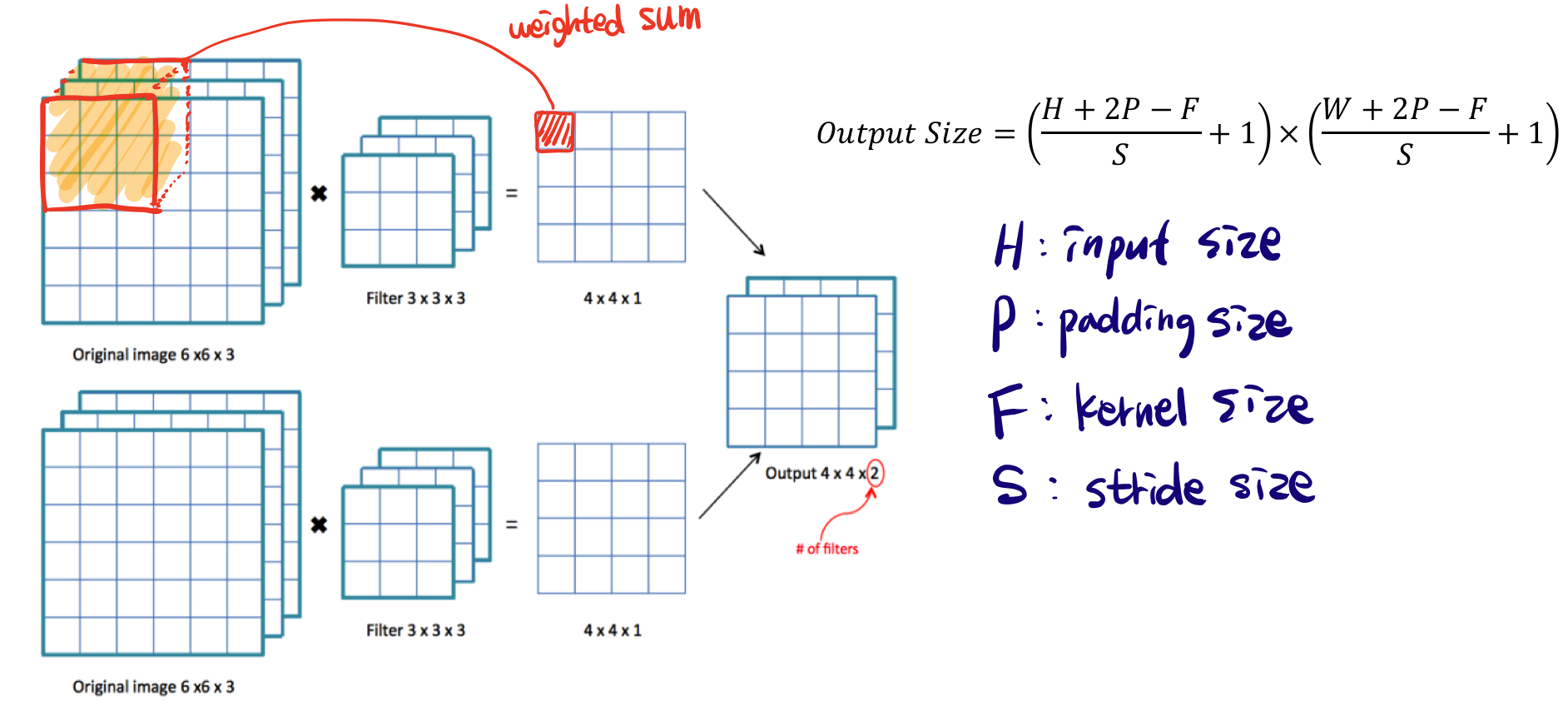
- convolution의 특징
1. input 노드와 output 노드의 연결이 fully가 아닌 local하게 연결되어 있음
2. parameter를 공유하게 된다. 아래의 그림을 통해 직관적으로 이해해보면, kernel이 3이고 stride가 1인
convolution과정 속에서 두 output 모두 동일한 weight를 사용하게 된다(sharing). dense layer의 fully connected는 input/output노드끼리의 weight를 다른 노드들 사이의 weight로 사용하지 않는다. 즉 일대일로 대응되는 weight만을 사용한다.
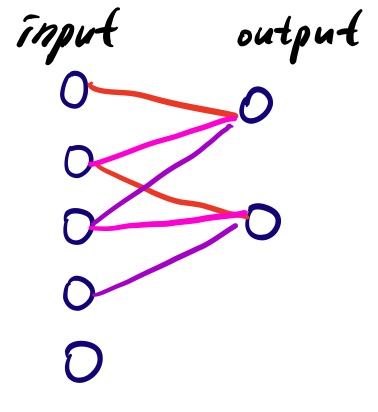
3. Equivariance to transition => convolution(shift(input)) = shift(convolution(input)) : input 의 특정node를 옮기고 convolution한 결과나 input을 convolution한 결과를 옮긴 결과나 같다는 말이다. 아래의 그림을 보면 왼쪽은 convolution을 하여 output 노드가 5, 10 순서로 구해져있고, 오른쪽은 input 노드의 위치가 바뀌어져서 convolution을 하게 된다. 결과는 Equivariance하다. 왜냐하면 convolution 이 local의 정보를 기반으로 weighted sum을 하기 때문이다.
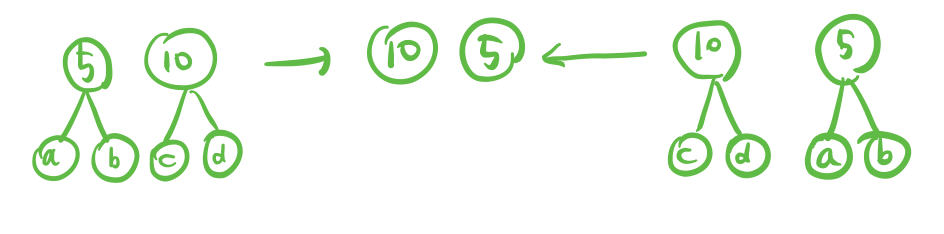
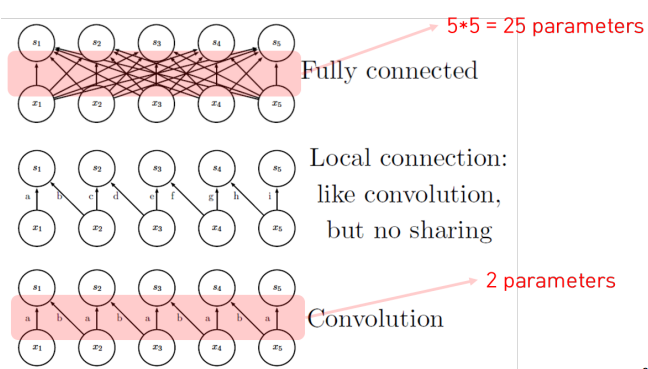
아래의 그림을 보면 convolution 을 fully connected 와 비교하면 추정해야 하는 parameter의 개수부터가 줄어드는 것을 알 수 있다.. 그 이유는 앞서 언급했던 것처럼 input노드는 parameter를 local 하게 본다는 점과 이 parameter를 sliding하면서 공유한다는 것이다.
Local connection 이라고 해서 convolution과 동일하게 local하게 연결되어 있지만 parameter가 sharing되지 않는 네트워크이다.
Pooling
pooling이라는 operation은 convolution에서 local하게 connecting을 하는데 이 때, local 영역의 값들의 대푯값(summary statistic)을 뽑아주는 operation이다.
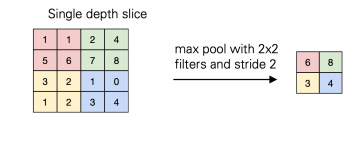
아래의 그림을 통해서 직관적으로 이해가 가능하다. max pool with 2x2라 되어있는데, max pooling은 영역에서 max값 하나만 뽑겠다는 것이다. average pooling도 있다.
pooling을 함으로써 주어진 local 영역의 크기를 줄인다. 즉, activation map의 크기가 줄어 든다는 것이다. 그러므로 stride도 2이상씩 주게 되며, filter를 옮겨다니면서 sliding하는 것이 convolution과 거의 유사하다. 가장 큰 차이점이라 한다면 각각의 activation map에서 독립적으로 operating이 실행된다는 것이다.
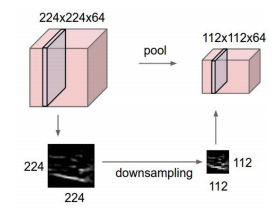
예를 들어 아래의 그림과 같이 112x112x64 activation map이 있다. 이를 pooling(filter=2x2, stride=2)하면 112x112x64 가 된다. 즉, width, length 축 말고 channel축은 변하지 않는다. convolution하면은 원래 1이 되는데 말이다. 이는 각각의 channel축에 독립적으로 작용한다는 것을 의미한다.
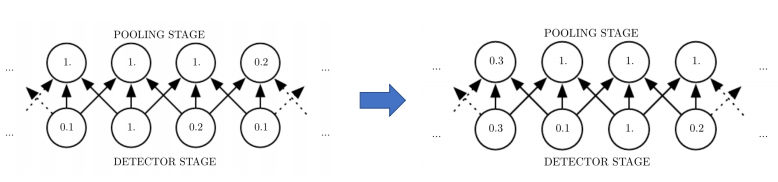
pooling의 성질은 Invariant to small translations of the input 가 있다. 이말은 input에 약간의 translation을 주어도 변하지 않는 다는 말이다. 예를 들어 아래의 그림 중 왼쪽을 보면, kernel이 3인 것에 대해서 1 dimension으로 pooling한다. 그러므로 3 개 중에 하나를 뽑은게 되는 것이다. 그리고 input이 오른쪽 처럼 한칸씩 shift되었다고 해보자. 여기서 shift는 translation 했다고 한다. 자, small translation이 발생했다. 이상태에서 pooling을 해보면 왼쪽, 오른쪽 모두 pooling stage 부분에 가운데 두개의 노드는 translation(여기선 shift)했음에도 값의 변화가 없는 것을 볼 수 있다. 왜냐하면 어차피 pooling이라는 것은 local영역에서 대푯값을 뽑는거기 때문에 window상에서 움직여봤자 invariant하게 된다.
요즘에 pooling operation은 많이 사용되진 않는다. 가장 큰 목적이 주어진 입력의 크기를 줄이는 것이기 때문이다. 이렇게 크기를 줄이는것은 convolution도 수행이 가능하다. stride에 2를 주면 절반정도로 줄어들게 할 수 있기 때문이다. 초창기에는 자주 이용했지만, 그냥 stride가 2이상인 convolution으로 대체하는 경향이 있다.
다음장에서는 직접 CNN를 구성해보도록 한다.
ref)
Applied Deep Learning - Part 4: Convolutional Neural Networks
Overview
towardsdatascience.com
ㅇSangheumHwang(Deep learning class)
'딥러닝' 카테고리의 다른 글
| multi-layer perceptron (0) | 2020.08.27 |
|---|---|
| Single Layer Perceptron (0) | 2020.08.06 |
| fundamentals of machine learning (0) | 2020.06.20 |
| regression (0) | 2020.06.20 |
| multi class classification (0) | 2020.06.20 |


댓글