Perceptron 은 신경망(딥러닝)의 첫 발자국으로써 매우 중요한 알고리즘이다. Perceptron은 소위 말해 여러개의 signal 신호를 받아서 하나의 출력값으로 만들어 내뱉는 방법이다. 학습을 통해서 데이터들이 놓인 분포를 linear boundary로 구분 짓게 된다.(classifiaction 의 경우).
Perceptron 중에서 single layer perceptron은 인경망 중에서도 활성화 함수로 임계값에 의해 출력값을 도출하는 간단한 형태를 말한다. 이번 장에서는 이 single layer perceptron을 classification 의 예시를 가져와서 어떤식으로 예측을 수행하는지 그 과정을 살펴보았다. ref에 포함된 강의 영상을 참조하였다. 쉬운 예제로 설명하기 때문에 그리 어렵지 않게 neural network의 구조를 이해할 수 있었다.
아래의 표는 Class가 각각 C1, C2인 과일들을 나타낸다. 변수는 Weight와 Length이고 4개의 case인 것을 확인할 수 있다. 주어진 parameter를 활용하여 single layer perceptron을 학습한다. 그리고 학습된 모델을 가지고 Weight가 140이고 Length가 17.9인 과일의 Class를 분류한다.

변수가 2개 이므로 axis가 2인 2차원 평면에 각 case를 뿌려볼 수 있는데, 각 Class C1과 C2를 잘 구분 지을 수 있는 class boundary를 찾아야 한다.

아래의 그림은 neural network의 구조이다.
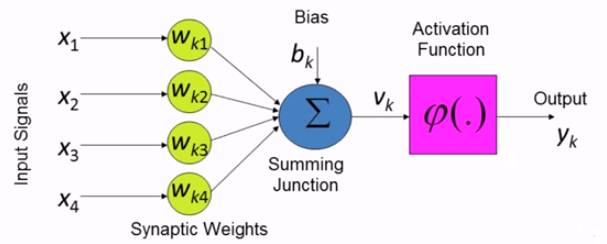
왼쪽부터 input vector, Weight vector가 보이며, 이어서 Summing Junction과 bias 그리고 Activation Function , Output이 있다.
perceptron 이라하면 선형적으로 분리된다고 할 수 있는 패턴의 분류를 위해 사용되는 neural network의 가장 간단한 형태라고 할 수 있다. 위 그림의 구조 자체라고 봐도 무방하다. 기본적으로 조작이 가능한 weight와 bias로 이뤄진 single neuron들로 구성되어 있다.
아래의 $u_{k}$는 input vector와 그에 대응되는 weight vector 간의 곱들을 더한 결과이다. 말 그대로 vector 간의 곱의 합이다.
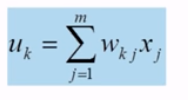
이 $u_{k}$에 bias를 더한 $u_{k} + b_{k}$ 이 $v_{k}$가 되고,
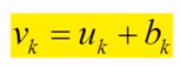
이 $v_{k}$을 Activation Function $\varphi $ 을 적용시켜 output 을 만들게 된다.
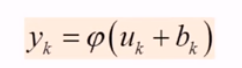
bias를 Summing Junction 에서 더했는데, 애초에 input vector의 가중치 벡터와의 곱을 하는 과정에서 미리 추가한다면 $u_{k}$ 에서 bias까지 합했다고 했을 때, 아래와 같이 나타낼 수 있다. $j$가 0부터 시작하게 되고, 이 때 0번째는 bias 에 해당하는 번호이다. $j$=1부터 input node number 이다.
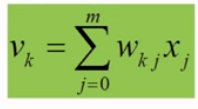
아래의 그림을 보면 bias가 $x_{0}$에 위치한 것을 확인할 수 있다. 기본적으로 bias vector는 fixed input으로 여기선 일단 +1을 해주고 시작한다.

neural network 구조에 포함된 도구들에 대해서 알아보자.

$X(n)$은 input vector 이다. $m$은 쉽게 말해 독립변수의 개수라고 생각하면 되고 +1은 bias vector 때문에 해준 것이다. $n$개의 input vector를 보았고 col vector를 row vector형태로 표현해둔 것이다.
다음으로 가중치 벡터 weight vector 역시 input vector 와 동일하게 설계가 되어 있는 것을 알 수 있다. $b_(n)$은 bias weight vector 이다. y(n)은 $X$와 $W$들의 곱의 합(summation) 이후 activation function 을 거쳐서 나오는 output 을 말한다. 즉, $n$ 케이스의 실제 값(label)을 말하고, $d(n)$은 예측 값이라고 할 수 있다. neural network가 잘 train 된다면 actual response와 desired response가 같아지게 된다. 다를 경우 계속 retrain 하게 되는 것이다. 마지막으로 learning-rate $\eta $ 가 있다.
예제를 통해 initial weight와 bias를 수정해나가는 solution을 파헤쳐보자. 원래 weight를 random 하게 부여해서 시작한다.
우선 여기 예제에서 $w$는 어느정도 train 이 되어 있는 weight 들이다. 다만 새로운 데이터에 대한 예측을 진행하는 과정에 초점을 맞춘다.

알려지지 않은 데이터 $x_{1} =140$과 $x_{2} = 17.9$가 주어졌다. 그렇다면 위의 그림의 $x(unknown)$은 input vector로써 bias +1을 포함하는 vector가 되겠다. $w(3)$은 weight vector이며, 괄호 안의 3은 업데이트를 진행 단계라고 봐도 무방하다. (update가 되던 안되던 횟수는 올라간다.) 약간의 train 을 거친 weight값이라고 명시하였기 때문에 여기서는 4번 거쳐진 weight를 사용한다고 할 수 있다.
이어서 input vector와 weight vector간의 곱의 합을 $sgn()$ 속에 넣는 Activation Function 작업을 진행해준다. activation function 은 classification에서 numerical한 결과값을 class 범주에 매칭해주기위해 한번 mapping을 해주는 함수이다. 특정 범위의 포함된 값을 해당하는 class에 매칭해주는 역할이다. 이 Activation function에 대한 것은 다시 다루도록 하겠다.
output은 input X weight vector 의 summation 값 1220에 activation function을 적용한 결과 1이 나와서 이 unknown $x$는 class C1에 속한다고 예측하게 된다.
이번에는 모델의 weight를 수정하는 과정이 어떻게 돌아가는지에 포커스를 맞춰보자.
가장 위 표에서 첫번째 케이스부터 하나씩 learning에 적용시켜본다.
$W$ vector는 앞의 예제와 같으며, bias 만 50에서 -1230으로 바뀌어진 상태에서 시작한다.
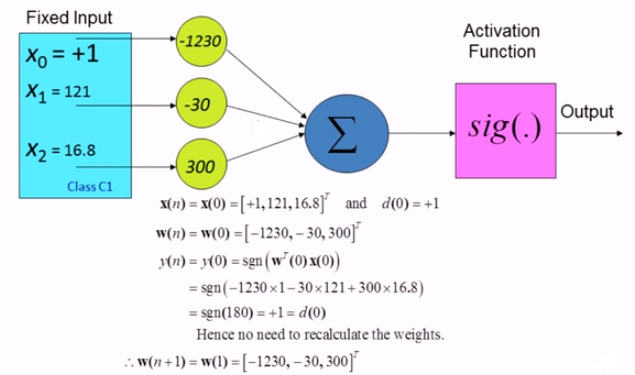
(x1, x2)가 (121, 16.8)일 때 Class C1에 속한 첫번째 케이스이다. 페이지 가장 위 표에 있는 학습 데이터 중 하나의 케이스이다. $X$와 $W$ 곱의 합을 구한뒤 역시 Activation Function을 거친다. 그 결과가 1이 나오고 원래의 desired response인 $d(0) = 1$ 과 같기 때문에 weight를 수정하지 않는 결론을 내리고 종료한다.
두번째 케이스에 대한 input vector를 가져왔다. 이번에는 (x1, x2)가 (114, 15.2)인 케이스이다. 바로 위의 과정과 마찬가지로 layer를 거쳐 output을 보니 desired response와 다른 값이 나왔기 때문에 weight를 수정하는 결론을 내리고 weight 수정에 들어가게 된다.
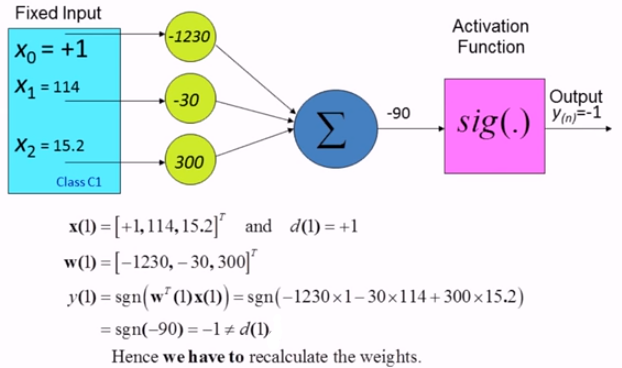
weight를 수정하는 과정에는 우리가 처음에 hyperparameter로 설정한 learning rate인 $\eta$ 값 0.01을 가져와서 사용하게 된다. 업데이트된 weight를 $w(n+1)$라하면 기존의 $w(n)$에 update할 값을 더해준다. update하는 값은 $\eta$ (learning rate) X $[d(n) - y(n)]$ (error) X $x(n)$ (input vector) 이다. 이를 수행해주면 $w(1)$ weight vector가 $w(2)$와 같이 update된 모습을 볼 수 있다.
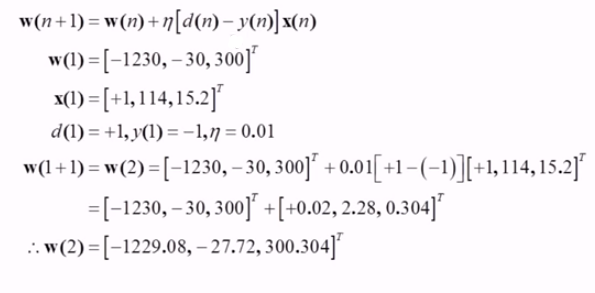
이제 세번째 케이스인 (210, 9.4) 는 $w(2)$ 가중치를 물려받았고 이를 토대로 learning을 시켜보자.

세번째 케이스인 (210, 9.4)에 대해서는 desired response와 actual response가 일치하여 weight를 update하지 않고 넘어가는 결론을 내리게 된다.
그리고 네번째 케이스는 (x1, x2)가 (195, 8.1)인 케이스이다. 역시 물려받은 $w(3)$을 토대로 learning을 진행한다. 아래의 계산 결과를 보면 알겠지만, 이 번 케이스 역시 weight를 update할 필요가 없다는 결론이 나왔다.
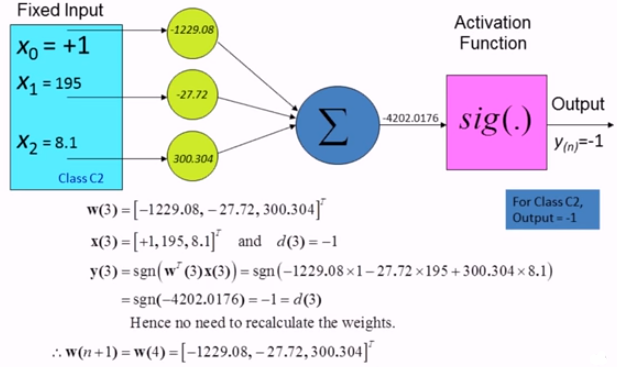
일단 여기까지 네개의 케이스를 모두 넣어보면서 weight를 update하는 과정을 한번 진행하였다. 여기서 우리는 아까 weight를 update진행했는데, 그렇기 때문에 잘 분류를 하는지 recheck를 할 필요가 있다.
이어서 $w(4)$를 가지고 다시 첫번째 케이스 부터 살펴본다. 아래의 그림에 나와있듯 update가 필요없다는 결론을 얻는다.

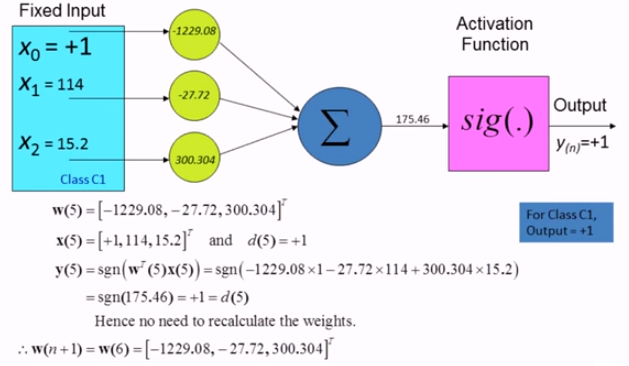
계속 이어서 $w(5)$을 가지고 두번째 행에 대해 진행한 결과 weight update를 하지 않아도 된다는 결론을 얻었다. 이것이 의미하는 것은 train 데이터로 classification을 잘 해줄 수 있는 decision boundary를 완성했다고 보면된다. 이제 이 boundary를 가지고 unknown data에 대한 예측을 수행하면 된다.
우리가 만든 decision boundary 는 linear combination $-27.72x_{1} + 300.304x_{2} - 1229.08 = 0 $으로 나타낼 수 있으며 아래의 그래프와 같이 영역을 나눌 수 있다.
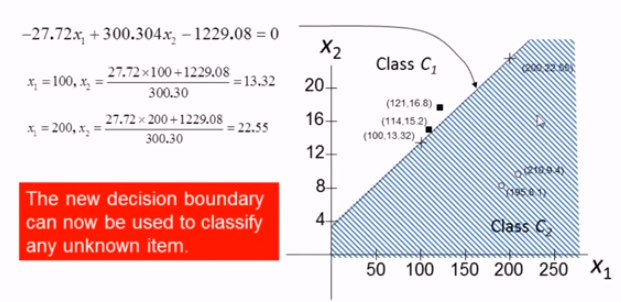
boundary $-27.72x_{1} + 300.304x_{2} - 1229.08 = 0 $ 에다가 unknown data를 대입하여 scalar를 구하고, Activation Function 을 거치게 되면, 결괏값을 토대로 class C1으로 분류하게 된다.

ref)
1. https://www.youtube.com/watch?v=S3iQgcoQVbc
'딥러닝' 카테고리의 다른 글
| Activation Function (0) | 2020.09.24 |
|---|---|
| multi-layer perceptron (0) | 2020.08.27 |
| Convolution and Pooling (1) | 2020.06.27 |
| fundamentals of machine learning (0) | 2020.06.20 |
| regression (0) | 2020.06.20 |



댓글