LDA. 잠재 디리클레 할당. 주어진 문서에 대해 각 문서에 어떤 주제들이 존재하는지에 대한 확률 모형. 토픽별 단어의 분포와 문서별 토픽의 분포를 모두 추정.
검색 엔진, 고객 민원 시스템 처럼 주제 파악이 필요한 곳에서 사용된다. LDA는 토픽모델링의 대표적인 알고리즘이다.
LDA는, 문서들은 토픽들의 혼합으로 구성되어져 있으며, 토픽들은 확률 분포에 기반하여 단어들을 생성한다고 가정한다. 데이터가 주어지면, LDA는 문서가 생성된던 과정을 역추적한다.
LDA수행시 토픽이 몇 개가 존재할지 가정하는 것은 사용자가 해주어야한다. 즉, 토픽 개수를 지정해주는 것이다. 이렇게 하이퍼 파라미터 값을 선택해주면 LDA는 각 문서의 토픽 분포와 각 토픽 내의 단어 분포를 추정한다.
아래의 그림은 논문인가, 게재된 LDA를 설명할 때 자주 쓰이는 그림인데, 이 그림을 통해서 LDA가 보여주려 하는 것을 파악해 볼 수 있다. 우선 가장 오른쪽에서 보여지는 그래프로 토픽들은 문서에 토픽들이 색깔별로 저렇게 분포한다고 말해주고 있고, 그다음 가장 왼쪽에 토픽 내에 단어들의 분포를 나타내주게 됩니다.

노란색 토픽안에 gene이라는 단어가 등장할 확률은 0.04, dna는 0.02, genetic은 0.01이다. 주어진 문서를 보면 가장 오른쪽 막대그래프를 통해서 노란색 토픽이 가장 많음을 알 수 있다.
바로 이 우측에 있는 Topic proportion(토픽 비율)과 assignments(할당)이 LDA의 핵심 프로세스이다.
문서 집합에서 얻은 토픽 분포로부터 토픽을 뽑는다. 이후에 해당 토픽에 해당하는 단어들을 뽑는다. 이것이 LDA가 가정하는 문서 생성과정이다.
실제 문서에 보이는 단어들이 드러난 정보지만 어떤 토픽에서 뽑힌 단어인지는 알 수가 없다. 따라서 이러한 이면에 존재하는 정보 (잠재된 정보)를 추론하는 것이 LDA이다.
아래의 그림은 LDA의 모델 아키텍처이다. 여기서 D는 전체 문서의 개수, N은 문서 d에 포함된 단어의 개수, K는 전체 토픽 수 (하이퍼 파라미터) 이고, 이 네모안에서 각기 수만큼 반복하라는 의미이고, 동그라미는 변수를 나타낸다.
우리가 관찰이 가능한 변수는 d번째 문서에 등장한 $n$번째 단어 $W_{d,n}$이 유일하다.
이 정보만을 가지고 하이퍼 파라미터(사용자지정) $\alpha$, $\beta$를 제외한 모든 잠재 변수를 추정해야한다.
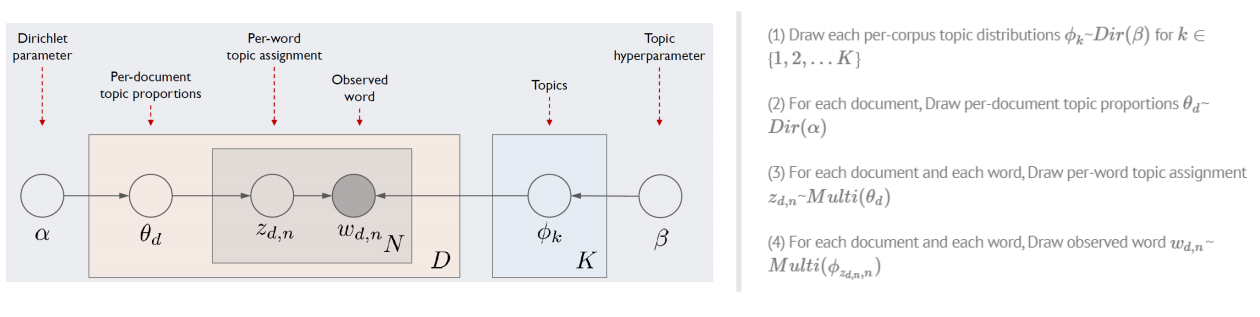
-$\phi_{k}$는 $k$번째 토픽에 해당하는 벡터, 말뭉치 전체의 단어 개수만큼의 길이를 가짐.
-$\phi_{1}$는 아래 표에서 첫번째 열. 마찬가지로 $\phi_{2}$는 두번째, $\phi_{2}$은세번째 열벡터
-$\phi_{k}$는 하이퍼 파라미터 $\beta$에 영향을 받는다.(디리클레 분포)

-$\theta_{d}$는 $d$번째 문서가 가진 토픽 비중을 나타내는 벡터 $\phi_{1}$은 아래표에서 첫번째 열.
-$\theta_{1}$은 아래 표에서 첫번째 행벡터, $\theta_{5}$는다섯번째행벡터
-$\theta_{d}$ 역시 하이퍼 파라미터 $\alpha$에 영향을 받음

서울 과기대 이영훈교수님 강의와 여럿블로그(wikidocs.net, ratsgo's blog)를 참조하였음을 명시합니다.
'NLP' 카테고리의 다른 글
| 트위터 데이터 수집 (a.k.a twitterscraper) (0) | 2020.02.05 |
|---|---|
| 비정형 데이터 - Doc2Vec (0) | 2019.12.19 |
| 비정형 데이터 - GloVe (0) | 2019.12.16 |
| 비정형 데이터 - Word2Vec (0) | 2019.12.16 |
| 비정형 데이터 - Classifier_Basic (0) | 2019.12.16 |



댓글