이번장에서는 단어 임베딩 기법 word2vec을 알아본다.
Word2Vec
텍스트를 딥러닝에 인풋으로 넣을 수 없다. 하지만 숫자는 인풋으로 넣을 수 있다.
텍스트를 숫자로 만들어라.잘. 임베딩.
원핫인코딩같은게 자주 사용되는데, 이런거는 유사도가 없고 수치는 의미가 없다.
그래서 인코딩 대신에 임베딩을하게 된다.
임베딩을 하게 되면 차원도 저차원이고, 유사도를 가질 수 있게 된다. 그 임베딩을 하는 첫 단추가 word2vec 방법이다.
word2vec은 중심단어와 주변단어 벡터의 내적이 코사인 유사도가 되도록 단어벡터를 벡터공간에 임베딩한다고 한마디로 요약을 합니다. 이 말은 내 주변에 단어들이 학습을 거치면 이제 텍스트가 아닌 벡터 수치로 여전히 가까워 보이게 남기는 것이라고 할 수 있을 것 같다.
우선 복잡한 수식보다는 아주 쉬운 예로 천천히 살펴보도록 하겠다.
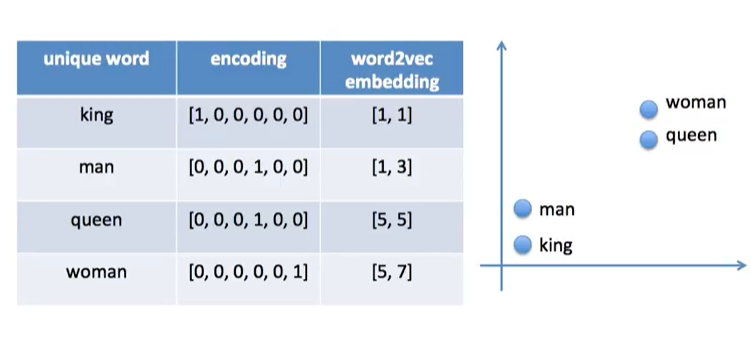
아래의 그림은 그렇다 단어x단어 행렬을 '원-핫-인코딩' 한 것이다. 독립적인 벡터로 '인코딩' 한 것이다.
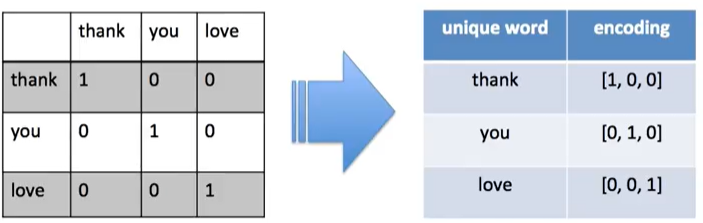
아래의 그래프 처럼 원 핫 인코딩은 모든 벡터간의 거리가 동일하다. 각도도 전부 90도로 유사한걸 찾을 수가 없다.

임베딩을 사용한다. 차원이 적어지도, 유사도를 가질 수 있게 된다.
아래의 표처럼 4차원에서 2차원으로 저차원으로 줄인 것을 볼 수 있다.

word2vec은 비슷한 위치에 있는 단어들 사이에서 유사도를 얻을 수 있다.
아래의 그림은 skip-gram에서 window를 1로 한 경우. 해당 단어의 좌우 한개씩의 단어만 체크 한다. 컴터가 워드랑 타겟값을 만든다.
그런 의미에서 사람들은 unsupervised-learning이라고 하거나 self-learning이라고 한다.

아래의 표처럼 윈도우 크기를 2로 할 경우 해당 단어의 좌우 각각 두개씩 단어를 고려한다.

아래의 표는 위의 표에 있는 두 열을 쫙 갈라서 각각 원핫인코딩 벡터를 표시해본 것입니다.
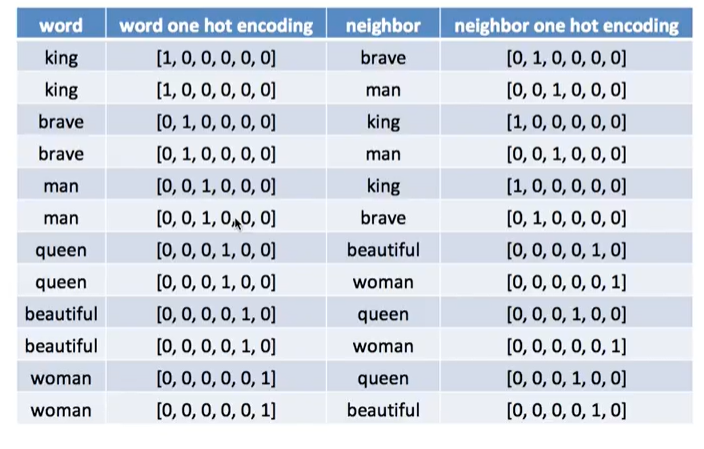
위의 표에서 인코딩된 수치형 열만 가져와서 아래의 그림처럼; 그래서 이 값들을 input과 target으로 두고 hiddenlayer에서 행렬을 구하라고 시키게 됩니다.

아래의 그림은 word2vec 임베딩 값을 얻기위한 딥러닝 모델의 아키텍처이다. 총 3개의 층이 있는 것을 확인할 수 있다. input, hidden, output layer가 있다. 아래의 그림에서는 우선 예로 king 단어를 가져왔고, 원-핫-인코딩이기 때문에 벡터의 차원($V$)은 단어의 개수가 된다. 즉 지금은 총 6개의 차원이다.
hidden층에는 노드가 2개 뿐이다. 이는 사용자가 지정해주어야 하는 부분이다. 왜냐하면 hidden층이 word2vec이 될 것이기 때문에 지정을 해줘야한다. 차원의 수를 정해준다고 생각해도 된다. 원-핫-인코딩보다 적은 차원의 벡터를 갖게해서 유사도를 가질 수 있게 하기 위함이다.

아래의 그림 king([1,0,0,0,0,0])의 이웃은 brave였고, brave 같은 경우에는 [0,1,0,0,0,0] 이다.
input이 들어가고, hidden층에 "어떤값"(초기에는 랜덤하게 주는 것 같음.)이 들어가고, 그다음 아웃풋으로 소프트맥스(softmax)를 취한다(소프트 맥스 값으로 얻은 값들의 합은 1이다.).
이제 아래의 그림처럼 아웃풋 값과 타켓벨류 간의 차이 값을 가지고 크로스 엔트로피를 계산함으로써 back propagation을 실시한다. 그래서 점차적으로 $w$값이 변하게 된다.

아래의 그림, king과 man의 경우.
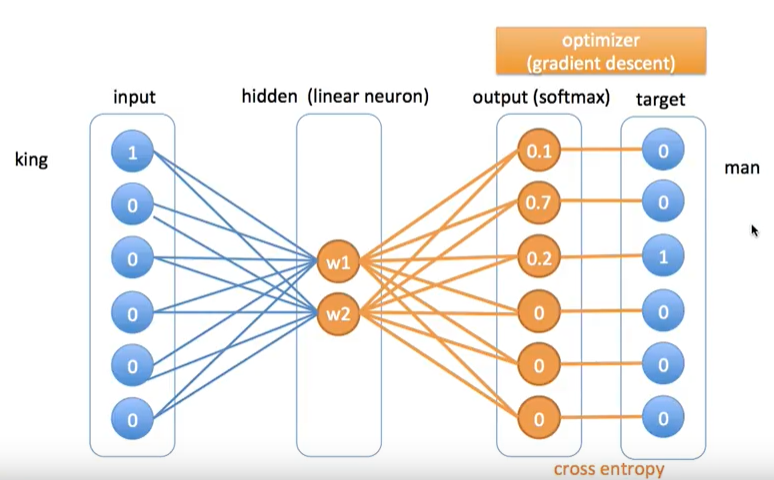
아래의 그림, brave와 man의 경우.

이렇게 계속해서 feed forward backpropagation을 하면서 점차적으로 w가 유사도를 갖기 위한 값으로 변하게 된다.
아래의 그림은 이제 $w$가 값을 최종적으로 갖게 된 상황이다.

아래의 그림처럼 2차원으로 된 $w$값인 임베딩 값을 얻었다.
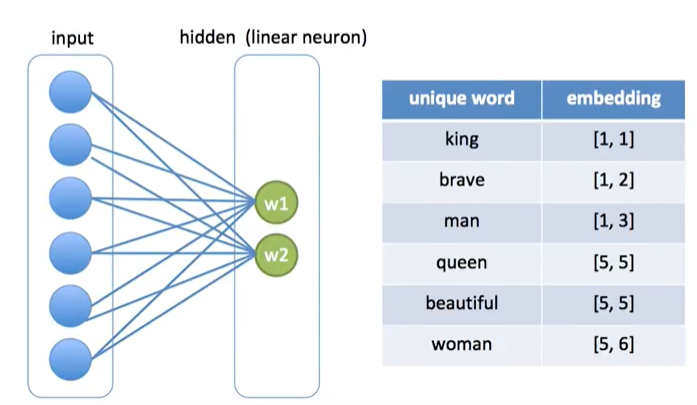
예를 들면, hidden층의 첫번째 레이블 값인 [1,1]이 임베딩된 값 즉, word2vec이 된다.

이제 아래의 그림처럼 바로 look-up table로 사용할 수가 있다. king-man, queen-woman이 가까운 위치에 있는 것을 알 수 있다.
인풋으로 $w$ (1x$m$)를 넣고 뭔지모를 hidden 층에서 내가 정한 차원($n$)에 맞는 행렬($m$x$n$)을 곱해서 output을 소프트 맥스를 적용하여 내고, window로 열심히 주변단어를 둘러보았기에 그 target벡터와 output 벡터를 비교하고, 그 차이를 가져다가 크로스엔트로피를 구하고 backpropagation을 통해 $w$값(word2vec값)을 내가 정한 계산량만큼 계산하면서 수정해서 최종적으로 그 hidden층에 있는 $w$를 임베딩 값으로 사용하여 단어들 간의 유사도를 비교해볼 수 있다.
여기서 소프트맥스와 크로스 엔트로피값에 대해 우선 짚고 넘어가야 한다. 그래야 output의 결과가 뭔지 알 수 있고, 또 target과의 차이를 비교하는 것도 이해하게 될 것이다. 쉽게 설명이된 wikidocs의 설명을 통해 배웠다.
Softmax(소프트맥스): 분류해야하는 클래스가 k라 할 때, 똑같이 k차원의 벡터를 입력받고, 각 클래스에 대한 확률을 추정한다. k차원의 값들의 합은 당연히 1이 된다.
1.수식으로 설명하기
아주 좋은 데이터인 iris데이터에서 품종 3가지를 분류하는 것을 예시로 들어 설명한다.
$k$차원의 벡터에서 $i$번째 원소가 $z_{i}$번째 클래스가 정답일 확률을 $p_{i}$로 나타낸다고 할 때, 소프트맥스 함수를 다음과 같이 정의한다.
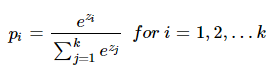
우리가 분류할 클래스는 3개이므로 k=3이 된다. iris로 부터 $z = [z_{1},z_{2},z_{3}]$의 입력을 받으면 아래와 같이 출력한다.
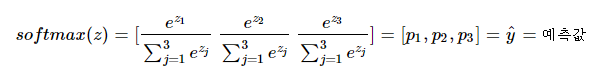
$[p_{1},p_{2},p_{3}]$ 는 각각 클래스가 1,2,3 일 확률 값으로 나타나게 되고, 확률이 가장 큰 클래스로 최종 분류하는 것이다.
---> 분류하고자 하는 클래스가 k개 일 때, k차원의 벡터를 입력받아서 k차원의 벡터에 클래스에 대한 각각의 확률 값을 리턴한다고 생각하면 간단하다.
2.그림으로 설명하기
아래의 그림에서 첫번째 질문인 '소프트맥스 함수의 입력으로 어떻게 바꿀까?' 위그림처럼 입력할 때 차원과 클래스의 개수가 다르다는 것을 알 수 있고, 이를 해결해야합니다.
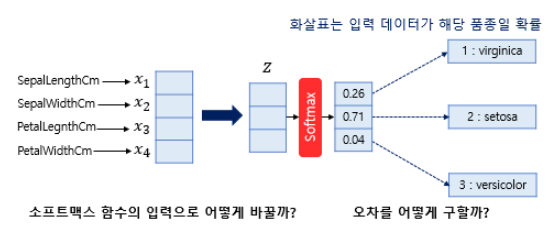
아래의 그림은 위의 그림에서 input에서의 벡터차원과 output에서의 벡터차원인 k가 서로 다른데, 이는 차원축소로 해결한다. 소프트맥스 함수의 입력벡터 $z$의 차원수만큼 결과값이 나오도록 가중치 곱을 진행한다. 아래의 그림에서 화살표는 (4 x 3 = 12)이며 전부 다른 가중치를 가지고 있고, 학습 과정에서 점차적으로 오차를 최소화하는 가중치로 값이 변경된다.

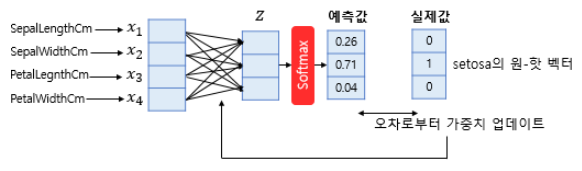
아래의 그림처럼 소프트맥스의 입력에 맞추어 차원도 축소했고, 이제 예측값을 얻어냈다. 소프트맥스 회귀에서는 실제값을 원-핫 벡터로 표현하여 이 값과 예측값사이의 오차를 구하게 됩니다.

선형 회귀나 로지스틱 회귀와 마찬가지로 오차로부터 가중치를 업데이트 합니다.

더 정확히는 선형 회귀나 로지스틱 회귀와 마찬가지로 편향 또한 업데이트의 대상이 되는 매개 변수입니다. 소프트맥스 회귀를 벡터와 행렬 연산으로 이해해봅시다. 입력을 특성(feature)의 수만큼의 차원을 가진 입력 벡터 $x$라고 하고, 가중치 행렬을 $W$, 편향을 $b$라고 하였을 때, 소프트맥스 회귀에서 예측값을 구하는 과정을 벡터와 행렬 연산으로 표현하면 아래와 같습니다.

- 크로스 엔트로피 함수
소프트맥스 회귀에서는 비용 함수로 크로스 엔트로피 함수를 사용한다.
아래에서 $y$는 실제값을 나타내며, $k$는 클래스의 개수로 정의한다. $y_{j}$는 실제값 원-핫 벡터의 $j$번째 인덱스를 의미하고, $p_{j}$는 샘플 데이터가 $j$번째 클래스일 확률을 나타낸다. 표기에 따라서 $\hat{y}_{j}$ 로 표기하기도 한다.

n개의 전체 데이터에 대한 평균을 구한다고 하면 최종 비용 함수는 다음과 같이 나타난다.

서울과학기술대 이영훈 교수님 강의, ratsgo blog, 허민석 유투버의 자료를 거의 다 베끼다시피 필기하고 있음을 명시합니다.
'NLP' 카테고리의 다른 글
| 비정형 데이터 - LDA (0) | 2019.12.16 |
|---|---|
| 비정형 데이터 - GloVe (0) | 2019.12.16 |
| 비정형 데이터 - Classifier_Basic (0) | 2019.12.16 |
| 비정형 데이터 - LSA / pLSA (0) | 2019.12.16 |
| 비정형 데이터 - TF-IDF (0) | 2019.12.16 |




댓글