지니불순도(Gini impurity)

 지니불순도라는 것은 데이터 분석에서 흔히 의사결정나무에서 사용되는 클래스개수에 따른 케이스들의 불순한 정도를 나타내는 척도라고 생각하면 될 것 같다. 지니불순도가 필요한 이유는 의사결정을 하는데 있어서 최적의 분류를 위한 결정을 계속해서 맞이하는데 이 결정에 사용되기 때문이다. 이 변수로 인해서 분류를 거쳤을 때 지니불순도가 얼마나 되는가? 를 생각할 수 있게된다. 또다른 불순도지표로는 엔트로피가 있다.

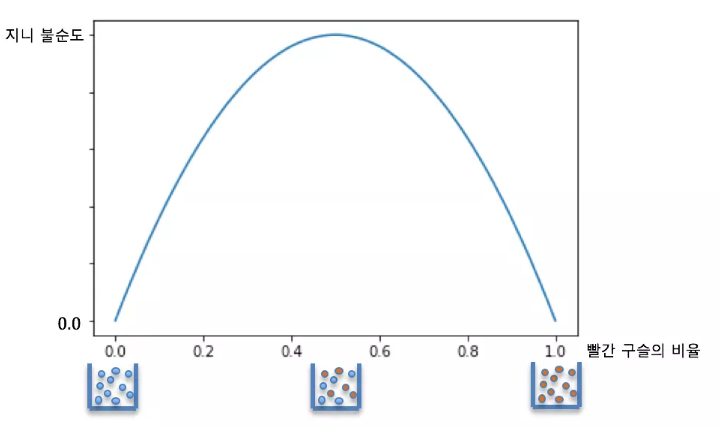
위의 그림 하나로 이해가 완전히 쉬워진다. 지니 불순도는 클래스안에 분류가 완벽하게 잘 되어 있으면 아래의 공식에 따라 0 이 된다. 즉 불순물없이 깨끗하게 분류가 되어 있다는 것이다. 하지만 섞이게 되면 0보다 큰 값을 가지게 되고, 최댓값은 0.5 이다. 

 이를 구하는 공식은 $1 - \sum_{j=1}^{J}(p_{j}(1-p_{j}))$ 와 같다.  $p$ 는 0~1 사이의 값을 가지는 확률 값인데 위의 예제를 들면, 파란 구슬이 들어있는 비율 $p$ 빨간 구슬의 비율 $(1-p)$ 라고 보면 된다. 이 식을 토대로 예를 들어 보자.

 

만약에 구슬 10개 중에서 파란구슬이 3개가 있다면 지니불순도는 어떻게 될까?

 

$ 1 - ( (\frac{3}{10})^{2} + (\frac{7}{10})^{2} ) = 0.42$ 로 지니계수가 0.42가 되며 42% 정도의 불순도를 구한다. 앞서 말했듯 지니계수는 의사결정나무에서 변수를 토대로 종속변수의 클래스를 분류하기 위해서 매 가지마다 지니계수를 활용하여 독립변수를 쪼개며 케이스들을 갈라나간다. 

 

 

그림출처: https://smalldataguru.com/%EA%B2%B0%EC%A0%95-%ED%8A%B8%EB%A6%ACdecision-tree%EC%9D%98-%EC%A7%80%EB%8B%88-%EB%B6%88%EC%88%9C%EB%8F%84gini-impurity%EB%9E%80-%EB%AC%B4%EC%97%87%EC%9D%BC%EA%B9%8C/

불러오는 중입니다...