이번 장에서는 아래의 포스팅 처럼 2가지 논문을 요약했던 것 처럼 또 2가지 논문을 살펴본 내용을 간략하게 요약하고자 한다.
Collaborative Filtering 에서의 유사도 지표 제안 논문.
Collaborative Filtering 에서의 유사도 지표 제안 논문.
CF 알고리즘에서 새로운 유사도 지표를 제안하여 기존 보다 나은 성능을 내도록 연구한 논문에 대한 간략한 정리. 이번 장에서는 2개의 논문에 대한 정리를 한다. 기존의 어떤 문제를 해결하
data-science-hi.tistory.com
1. Integrating Triangle and Jaccard similarities for recommendation (2017).
먼저 소개할 논문은 Integrating Triangle and Jaccard similarities for recommendation 이다. 이 논문의 경우 제목에서 보이는 것과 같이 Triangle 이라는 것과 자카드 유사도를 합쳐서 추천시스템에 활용하는 제안을 하였다.
자카드 유사도는 우리가 흔히 알고 있는 그 자카드 유사도가 맞다. 하지만 Triangle 이라는 것은 삼각형? 을 떠올리고 코사인 유사도? 식으로 생각해볼 수 있다. 그렇다. 코사인 유사도에서의 한계를 떠올려보자. 코사인 유사도는 두 벡터간의 각을 토대도 유사도를 산출해내는데, 이 때 단점이 예를 들어 [1,1,1], [5,5,5] 의 경우에는 유사도가 ' 1 ' 을 내뱉는다. 말이 안되는 유사도 값이다. 이는 각만을 고려하다 보니 생기는 문제이다.
코사인 유사도에서 각 벡터의 길이를 고려할 수 있다면 어떨까? 그 길이를 고려할 수 있는 것이 Triangle similarity 이다.
아래의 그림을 보면 벡터 OA 과 OB 를 잇는 벡터를 AB or BA 를 구한다. 최종적으로 Triangle 값은 삼각형의 넓이가 넓을수록 작은 값을 갖게 된다. 이 말인 즉슨, 벡터의 길이(length)를 고려할 수 있기 때문이다.
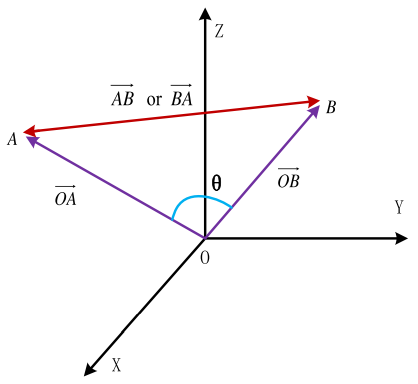
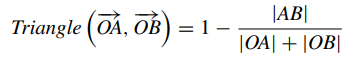
Triangle의 계산 같은 경우는 기존의 코사인 유사도의 식에서 분자부분에 내적이였던 부분을 pair wise 차이에 제곱합에 루트를 씌운 것으로 바뀐 것 뿐이다.
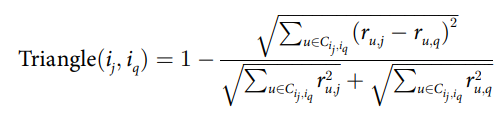
하지만 여전히 co-rated 가 1개일 때 가지는 한계는 여전히 존재한다.
최종적으로 제안하는 유사도는 위에서 구한 Triangle 과 자카드 유사도의 곱으로 나타내게 된다.
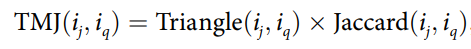
2. A new similarity measure using Bhattacharyya coefficientfor collaborative filtering in sparse (2015).
이번에 볼 논문은 Bhattacharyya 를 이용하여 유사도 지표를 만든다. 우선 Bhattacharyya 거리는 두 확률분포 사이의 거리를 측정하는 지표로써 신호처리, 이미지 처리, 패턴인식 연구에서 널리 사용된다. 위키에서 정의에 따르면 아래와 같이 이산확률분포와 연속확률분포에 대해서 각각 표현되고 있다.
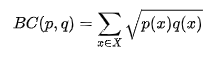

평점 행렬에서 Bhattacharyya 거리를 어떻게 구하는지는 예를 통해서 보면 쉽게 이해할 수 있다.
u1과 u2는 co-rated 평점이 존재하지 않는다. 이말은 유사도를 측정할 수 없다는 것이다. 바로 sparse problem 때문이라고도 할 수 있다. 하지만 Bhattacharyya같은 경우는 co-rated에 영향을 받지 않고 각자 user의 확률분포를 그릴 수 있고, 또 구한 확률분포를 가지고 서로간의 유사도를 표현해낼 수 있다.

아래의 식이 두 i, j 간의 거리를 구하는 것이다. $m$ 이 존재하는 확률변수라 할 수 있고, 각 확률변수들에 대한 추정된 확률값을 곱해서 루트씌운 값들의 합으로 표현된다.

당연하겠지만 확률분포의 가정 $p$는 0 이상이여야 하고, 모든 경우의 확률값의 총합은 1이 되어야한다는 전제가 아래의 수식이 말해준다.
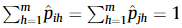
다시 이어서 위의 표를 토대로 거리를 구해보면 아래와 같다. 우선 $m$이 3으로 표시가 된 건, 두 i, j 가 가진 합집합 평점이 1,2,3 3개이기 때문이다.

이제 각각 1에 해당하는, 2에 해당하는, 3에 해당하는 확률값으로 각각 곱해서 루트한 것들의 합을 구하면 아래와 같이 1이 나온다.
이산형이기 때문에 직관적으로 설명이 가능한데, i와 j가 평가한 1, 2, 3의 비율이 모두 동일하다는 것이다.
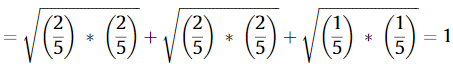
어렵지 않게 Bhattacharyya 거리를 구할 수 있었다.
Bhattacharyya 거리에 다가 $loc$라는 term을 곱하게 된다. 여기서 $loc$란 아래의 수식과 같다. 저자는 local similarity를 계산하기 위해서 아래와 같이 평균 대신 중앙값을 사용해서 local similarity를 표현하고자 하였다. 분모 하나하나는 각각의 표준편차를 의미한다.

최종적으로는 전에 Bhattacharyya 거리로 구한 유사도와 loc 지표의 곱과 기존 전통적인 방식의 자카드 유사도와의 합으로 새로운 유사도를 추출해낸다.

ref)
[1] Integrating Triangle and Jaccard similarities for recommendation,(2017) Shuang-Bo Sun, et al.
[2] A new similarity measure using Bhattacharyya coefficientfor collaborative filtering in sparse, (2015) Bidyut Kr. Patra, et al.
'추천시스템' 카테고리의 다른 글
| 딥러닝과 추천시스템 (0) | 2021.03.18 |
|---|---|
| Model based Collaborative Filtering (0) | 2021.02.04 |
| Collaborative Filtering 에서의 유사도 지표 제안 논문. (0) | 2020.10.29 |
| 추천시스템에서의 유사도 지표와 피드백 특징 연구. (0) | 2020.10.23 |
| 메모리 기반 CF 추천시스템의 문제점 (0) | 2020.08.23 |




댓글