추천시스템에서 널리 알려진 collaborative filtering(CF)는 주변 사용자들의 정보를 활용하여 추천을 하는 방법이다. 이번 장에서는 CF 알고리즘의 memory based 기반의 방법이 아닌 model based 로 하여금 CF 를 진행하는 방법에 대하여 알아보고자 한다.
아래의 그림은 model based CF 알고리즘에 대한 방법론들을 도식화 해놓은 그림이다. model based CF 방법들은 크게 클러스터링을 기반으로하는 알고리즘, 행렬 분해를 사용한 알고리즘, 그리고 성능이 가장 뛰어난 딥러닝 알고리즘으로 나뉘게 된다. 여기서 Matrix factorization 을 기반으로한 추천시스템의 알고리즘에 대해 알아보도록 한다.

먼저 기존의 memory based CF 추천시스템의 경우에는 주변 사용자와의 유사도를 토대로 주변의 이웃을 선정하여 가중 평균을 계산해 예측 평점을 구하는 방식으로 진행이 되었다. 하지만 치명적인 문제는 역시 sparsity problem 에서 나오는 수많은 결측값들이다. 주변 사용자의 정보를 활용함에 있어 가장 예측력이 좋게끔 하기 위해 최근접 이웃을 찾아야 한다. 이 때 사용되는 것이 유사도인데, 이러한 유사도 지표들은 모두 공통적으로 두 사용자 간의 공통 평가 항목이 적을 경우 성능에 치명적인 타격을 주게 된다. 이 문제에 대하여 결측값에 각 사용자의 평균으로 대체하거나 또는 전체 사용자의 평균으로 결측값을 대체하는 방법들도 연구되었다. 하지만 이러한 방법에도 성능을 끌어 올리는 연구에는 한계가 존재하게 되었고, 그 후 이러한 한계점을 개선하기 위해 등장한 것이 바로 model based CF 알고리즘이다.
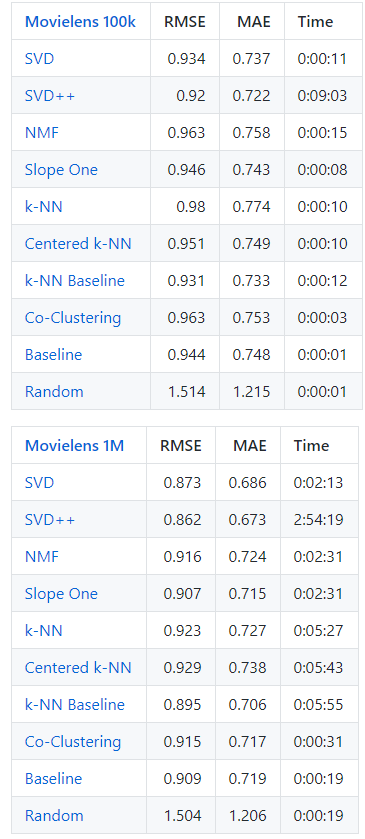
아래의 표는 추천시스템 성능 연구에서 대표적인 데이터셋으로 사용되는 Movielens 100k, 1M 데이터을 가지고 다양한 추천시스템 알고리즘으로 성능을 비교해본 결과이다. 아래에 보면 SVD, MMF 와 같은 model based CF 방법이 K-NN 과 같은 memory based CF 알고리즘보다 성능이 나은 것을 확인할 수 있다.
아래의 그림은 Matrix factorization 에 관한 그림이다. 그림에서 보이는 것 처럼 왼쪽의 카키색 행렬이 행렬분해로 인해 오른쪽의 분홍색 두 행렬의 행렬 곱으로 표현이 되도록 하며, 두 행렬 각각은 기존의 행렬의 행과 열에 대한 latent factor 를 가리키게 된다. 이렇게 분해된 두 행렬을 살펴보면, 먼저 두 행렬 중 왼쪽 행렬의 경우에는 Users 간의 유사도를 계산해볼 수도 있고, 오른쪽 행렬의 경우는 Movies 간의 유사도를 계산할 수도 있다. 각 행렬이 담고 있는 행 또는 열의 정보가 무엇인지 feature 를 정의할 수는 없지만, 이렇게 수학적인 행렬분해로 성질을 표현해낼 수 있다고 보면 된다.
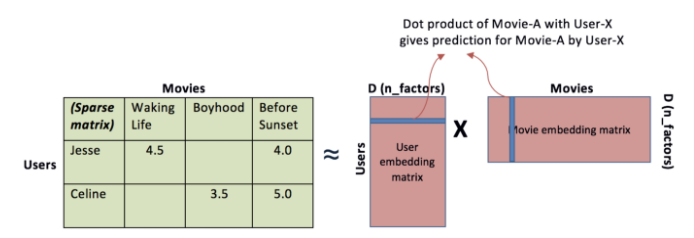
MF 에 대한 직관적인 설명을 잠시 살펴보자.
* 아이템 feature vector 는 input 으로 본다.
* 사용자 feature vector 는 weight vector 로 본다.
* 예측 평점 즉 예측값은 output 으로 본다.
* input 들이 고정이 되고, weight 들이 학습되는 선형회귀와는 다르게, 목적함수 SSE 를 최소화 하기 위해 weight 와 input 을 모두 학습한다는 차이가 있다.
1. (Singular Vector Decomposition)SVD
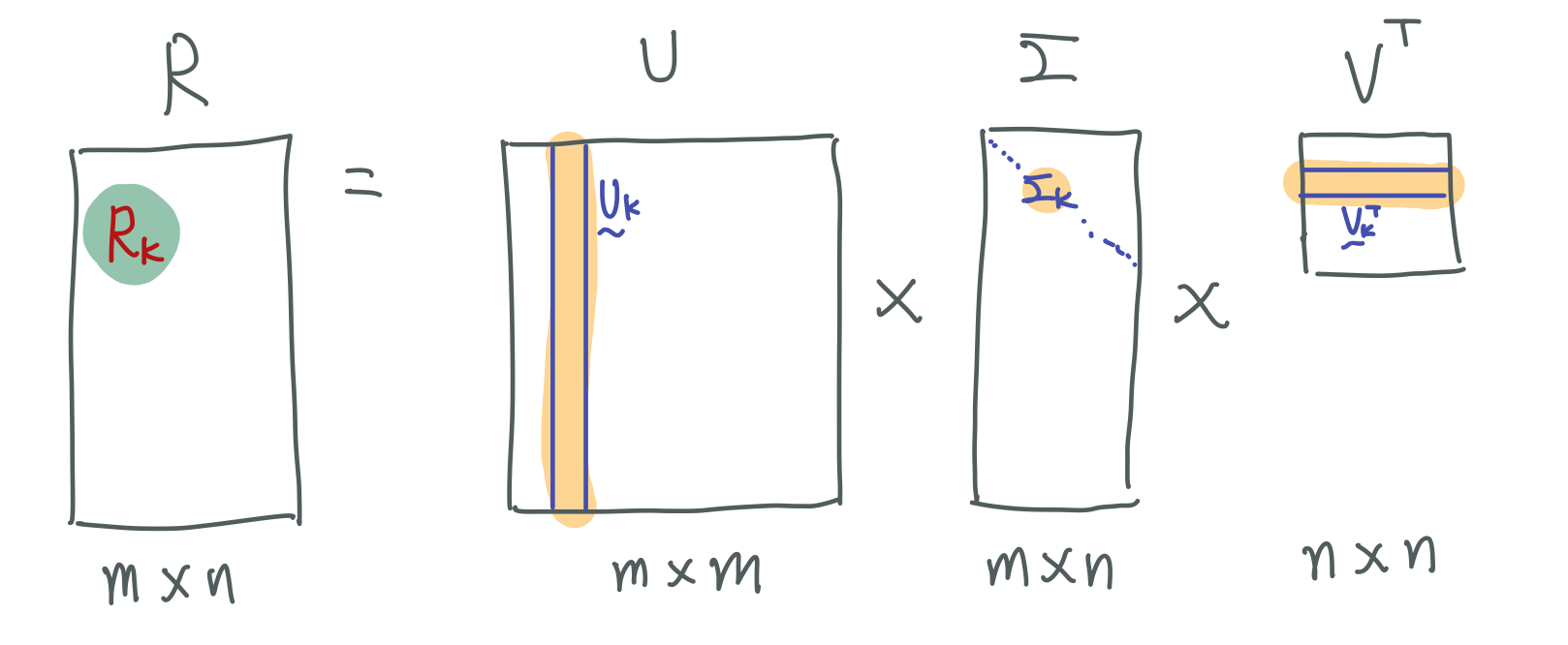
model based CF 알고리즘 중의 SVD 방법에 대해 알아보자. SVD 는 기본적으로 하나의 행렬을 $U, \Sigma, V^{T}$ 라는 세 개의 행렬로 분해하는 것을 의미한다. left singular matrix 인 $U$ 는 User 와 latent factor 간의 관계를 나타내며, $V$ 행렬은 Item 과 latent factor 간의 관계를 나타낸다. 그리고 가운데 시그마 행렬 $S$ 은 각 latent factor 의 정보를 담고 있다. 이 SVD 는 latent factor를 추출함으로써 원래 행렬 A 의 차원을 축소시킨다. 그래서 최종적으로 hyper parameter 로 축소할 행렬의 차원수(r) 만큼 축소시키게 된다. 그렇게 새로 탄생된 행렬은 역시나 user x item 이라는 정보를 담은 행렬이라고 할 수 있게 된다.
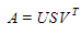
아래의 수식에서 $\hat{r}_{ui}$ 는 SVD를 통해 생성된 factorization 의 형태로 표현이 되고, 이는 $x$와 $y$ 간의 곱으로 형성이 되게 된다.
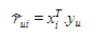
그리하여 기존의 평점인 $r_{ui}$ 와 $x, y$의 점곱으로 이루어진 $\hat{r}_{ui}$ 간의 차이의 제곱합이 곧 목적함수가 되고, 이를 최소화하는 방법으로 진행이 된다.

이어서 모델의 일반화 성능을 올리기 위해서 regularization term으로 L2 term 이 추가된다.

아래의 수식은 regularization term 과 bias term 을 추가한 최종 식에 해당한다. 예측 값과 실제 값 사이의 error 를 줄이기 위하여 bias term 을 추가한다. $b_{i}$는 아이템 $i$ 에서 전체 평균 $\mu$을 뺀 값들의 평균을 의미하고, $b_{u}$는 사용자 $u$ 에서 전체 평균 $\mu$을 뺀 값들의 평균을 의미한다.

add) SVD는 MF와는 명백히 다른 분석 기법이다. SVD 같은 경우에는 기존의 null 을 많이 포함하고 있는 sparse matrix에서 null 을 0으로 채우며, 최대한 이 값을 충실히 재현하도록 행렬이 분해되기 때문에 행렬을 재현해보면 0이었던 원소가 대부분 0에 가깝게 재현이 된다. 즉, 평가하지 않은 항목을 0으로 표시하고 평가한 값만 가지고 학습시킨 후 0의 값을 다시 예측값으로 계산할 수 없는 구조이다.
SVD 특성상 기존의 행렬을 3개의 행렬로 분해하여 다시 결합하여 재생시키는 것에 대한 재현율은 좋지만 원래 없던 값을 예측하는데에는 문제가 생기게 되는 것이다. SVD는 다른 분야에서 유용하게 많이 사용되지만, 추천 분야에서는 거의 사용되지 않는다. 🤦♂️🤦♂️🤦♂️🤣😂🤣😂
1. 기존 행렬에 대해 null 값을 0으로 채움.
2. $U, \Sigma, V^{T}$ 행렬로 분해.
3. latent factor matrix $\vec{u}_{k}, \sigma_{k}, \vec{v}_{k}$ 을 가지고서 예측값 $\vec{\hat{r}}_{k}$을 생성해서 실제값 $\vec{r}_{k}$ 과의 오차를 최소화하는 방식으로 진행한다.
2. Probabilistic Matrix Factorization(PMF)
우선 PMF는 데이터 셋에서 원소들이 특정 분포를 따른다는 전제하에 확률적인 방법으로 예측값을 추정하는 방법이다. parametric model 로 예측값을 생성해 내는데 과정에는 크게 Bayesian rule, MAP Estimation 등이 사용된다.
$U$와 $V$는 초기 행렬이 분해되어 나뉜 행렬들이고 이들이 모두 가우시안 분포를 따른다고 가정하고 진행한다.
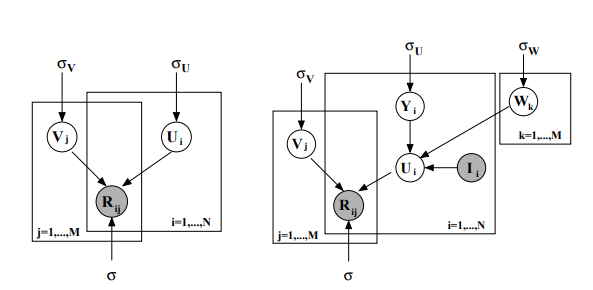
주어진 데이터 셋에서 원소들의 집합 R이 등장할 확률은 아래와 같은 수식으로 구성된다. 사용자와 아이템의 latent vector 의 곱한 값을 평균으로 사용하며, $\sigma^{2}$을 분산으로 한 정규분포들의 곱으로 구성된다. 위의 그림과 아래의 두번째 수식처럼 U, V 역시 가우시안 분포를 따르는 matrix 를 가정한다. 각각 평균과 분산으로 zero-mean, $\sigma$로 구성된다.


위의 정의한 식을 Bayesian rule을 활용하여 전개하고(생략), MAP(Maximum a Posterior) Estimation을 활용해 아래와 같은 식을 구성한다. 사용자, 아이템 feature로 얻어지는 posterior 분포의 로그 값이 아래와 같이 주어질 때, $C$는 parameter에 의존하지 않는 constant이다.
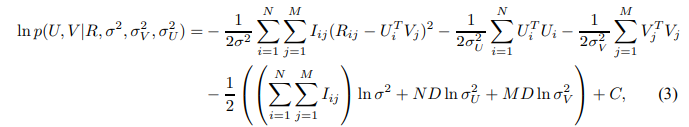
고정된 hyperparameter(observation noise variance와 prior variances)로 사용자, 아이템 feature 들로부터 얻은 log posterior를 maximizing 하는 것은 quadratic regularization term을 지닌 SSE 목적함수 부분을 최소화하는 것과 같다. 이차식의 특성상 $U, V$를 미분해 Gradient를 구하여 최적값을 찾아나간다.
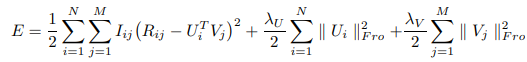
위의 식처럼 목적함수 $E$가 구성되면, 주어진 $R, \sigma^{2}, \sigma^{V}_{2}, \sigma^{U}_{2}$ 과 학습할 $U, V$를 활용하여 이 목적함수를 최소화시키는 parameter 를 찾게 된다. 그래서 아래와 같은 수식은 위에서 처음 봤던 식처럼 전개되어 예측값을 생성해내게끔 정리가 된다.

PMF 알고리즘의 경우 다른 알고리즘에 비해 성능이 좀 떨어지는데 이유는 사용가 간의 관계를 고려하지 않고, user x item 행렬만을 이용해서 예측했기 때문이다. 이에 user 간의 유사도를 preference에 따라 다르게 계산하는 방법등의 연구도 있다.
3. Non-negative Matrix Factorization(NMF)
SVD 와 더불어 행렬을 분해하여 원래 행렬과 최대한 유사하게 나타낼 수 있도록 하는 방법이 NMF 이다. 이 NMF 는 SVD 의 방법과도 그 맥락이 비슷하다고 할 수 있다. NMF 의 목표는 아래의 그림처럼 W와 H 의 dor product로 V를 approximate 하는 것이라고 할 수 있다. W x H 행렬의 차원은 V 행렬을 따라가거나 우리가 정한 차원으로 생성이 가능하다. 또한 특징으로는 W, H의 원소들과 V 의 원소들 모두 0 보다 큰 non-negative 한 값을 가진다. 왜냐하면 음수가 들어가면 방향까지 고려해야 하는데 이 알고리즘에는 벡터의 방향까지 고려하게끔 설계되지 않아 이에 해당되지 않는다고 생각한다.
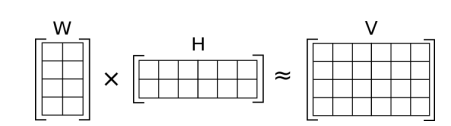
정확하게 초기 행렬을 재현해내는 것은 불가능하지만 최대한 가깝도록 최적화를 한다. 이 때 사용하는 것이 Frobenius norm 척도이고, 이는 벡터간의 거리를 잴 때 사용되는 유클리디안 거리를 행렬로 확장한 것이라 생각하면 된다.
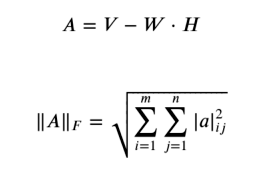
목적함수는 아래와 같이 설정이 되고, 초기의 행렬의 원소값인 실젯값과 W, H의 dot product로 이뤄진 행렬의 원소와의 차이의 제곱의 합 즉, SSE를 최소화 하는 방식으로 진행이 된다.

추천시스템에서 사용되는 평점 또는 사용자 피드백 데이터셋은 implicit 과 explicit data 로 나뉘게 된다. implicit 데이터의 경우는 주로 이진값으로 측정이 되어 있으며 이러한 데이터셋에서 NMF 와 같은 방법은 상대적으로 좋은 성능을 낸다고 알려져 있다.
add) 아래의 그림으로 MF 의 직관적인 이해를 다시 해보자. 먼저 latent factor의 개수 k 를 지정해준다. 이부분에 대한 연구도 있지만 다루진 않겠다. 사용자 직관이 들어가기도 한다.
k 를 정했다면 user의 개수 m, item의 개수 n을 오른쪽 진한 녹색 부분인 '임의의 행렬'로 구성해주고, 이 두 녹색의 곱을 가지고 예측 값을 생성하고, 원래 R 행렬의 실제 평점들과의 비교를 통해 녹색이 가진 원소들의 값들을 업데이트 시켜준다. SVD 와 동일하게 초기 R 행렬의 null 값에 대해서 0으로 채워주지만(무조건 0으로 채우지는 않는다, 평균과 같은 값을 넣어주기도 한다.)
SVD 와는 다르게 loss 를 계산할 때 실제값이 0인 경우에 대해서는 무시한 채 진행하기 때문에 실제로 평가한 값들과의 오차가 최소화되게끔 학습하여 P, Q 행렬의 원소들이 업데이트되기 때문에 성능이 SVD 와는 비교할 수 없게 좋으며 계산속도를 제외하면 준수한 성능을 보이는 알고리즘이다. 다만 단점으로는 새로운 user 혹은 item이 생겨나고 rating이 추가될 때마다 모든 연산을 처음부터 수행하여 모델을 만들어야 한다는 점이 있다. 👏👏

implicit data 예측 알고리즘 중에서 상위에 해당하는 것이 Weighted Regularized Matrix Factorization(WRMF) 알고리즘이다.
ref)
towardsdatascience.com/various-implementations-of-collaborative-filtering-100385c6dfe0
Various Implementations of Collaborative Filtering
Comparison of different methods to build recommendation system using collaborative filtering
towardsdatascience.com
github.com/NicolasHug/Surprise
NicolasHug/Surprise
A Python scikit for building and analyzing recommender systems - NicolasHug/Surprise
github.com
www.sallys.space/blog/2018/05/16/intro-to-resys/
medium.com/logicai/non-negative-matrix-factorization-for-recommendation-systems-985ca8d5c16c
www.notion.so/Non-negative-Matrix-Factorization-ed59fdf1616b471495265c7ab33aec32
rdrr.io/github/dselivanov/reco/man/WRMF.html
Mnih, A., & Salakhutdinov, R. R. (2007). Probabilistic matrix factorization. Advances in neural information processing systems, 20, 1257-1264.
'추천시스템' 카테고리의 다른 글
| 추천시스템 기술 요약 (0) | 2022.11.13 |
|---|---|
| 딥러닝과 추천시스템 (0) | 2021.03.18 |
| Collaborative Filtering 에서의 유사도 지표 제안 논문(2). (0) | 2020.11.09 |
| Collaborative Filtering 에서의 유사도 지표 제안 논문. (0) | 2020.10.29 |
| 추천시스템에서의 유사도 지표와 피드백 특징 연구. (0) | 2020.10.23 |




댓글