CF알고리즘에서 메모리 기반의 kNN 알고리즘에서 주요 이슈로 기본적으로 cold-start가 있고, 그리고 또 동시 평가 아이템을 기준으로 유사도를 구하는 알고리즘의 특성상, 동시 평가 아이템이 적을 수 밖에 없는 평점 매트릭스에서 더 잘 유사도를 구하기 위한 연구들에 대해 알아본다.
주어진 평점 매트릭스는 늘 sparse하다. 그럴 수 밖에 없는 것이 아이템은 제한되어 있고, 사용자는 상대적으로 훨씬 많다. 특정 사용자 둘 간의 유사도를 구하려해도 동시에 평가한 항목들이 소수여서 제대로 유사도가 측정되지 않는다.
이를 개선하고 싶으면 먼저, 유사도를 구하는 방법들에 대해 탐구할 필요가 있다. 유사도를 구하는 식은 다양하며 각 유사도가 가진 특징을 보고 적절히 발전을 시키면 기존의 base similarity measure보다 나은 성능을 보일 수 있기 때문이다.
유사도에 대한 특징을 정리하고, 이를 변형한 사례들도 함께 알아본다. 이후에는 사용자가 아이템에 내린 feedback(평점 내지 클릭여부)에 정성적인 의미를 담은 수치로 유사도를 더 잘 표현할 수 있게 하는 방법들에 대해서도 알아본다.
1. 추천시스템을 위한 유사도 측정 방법.
1.1 Pearson correlation coefficient(피어슨 상관계수)

흔히 양적 변수들 사이의 선형관계를 확인하기 위한 방법으로 사용되는 것으로 잘 알려져 있다. 코사인 유사도의 평점 부분에 각 유저의 평균값(not only co-rated feedback)을 뺀 term을 확인해볼 수 있다.
문제점: 코사인 유사도와 마찬가지로 벡터가 지닌 스칼라들의 scale에 대한 고려를 하지 않는다는 점이 있다.
또한 $r$벡터가 가진 feedback들이 모두 동일한 경우에는 0이 되어버려 최종 값이 nan으로 나오게 되는 문제가 있다. 그리고 $r$벡터가 1차원이게 되면 $r$벡터 값이 평균이 되어 마찬가지로 분자가 0이 되어 최종 값이 nan으로 나오게 된다.
정리하면 1. co-rated 아이템이 적은 경우 성능에 안좋은 영향을 미친다. 2. feedback 점수가 심각하게 차이가 있음에도 높은 유사도를 준다. [6] 3. 값의 절대적인 크기를 고려하고자 할 때 쓰이는 좌표 거리이다.
PCC 에서 파생된 Constrained Pearson's Correlation Coefficient (CPCC). PCC와는 다르게 분자와 분모에 평균대신 중앙값을 사용한다. correlation 이 증가하기 위해선 두 사용자의 rating 쌍이 둘 다 positive이거나 negative 인 경우여야 한다.
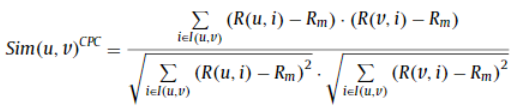
1.2 Cosine Similarity(코사인 유사도)

문제점: 두 벡터사이의 코사인 각의 크기를 가지고 유사도를 수치를 제시한다. -1 ~ 1 사이의 실수값을 가지며 -1에 가까울수록 반대되는 경우, 0에 가까울수록 서로 독립적인 것을 뜻하며, 1에 가까울 수록 같은 경우를 말한다. feedback의 경우 $r$에 대체적으로 양수만 들어가니 0~1사이의 값만 얻게 되는 경우가 흔하다.
코사인 유사도는 두 벡터간의 각을 고려한 수치이기 때문에 scale이 무시되는 경우가 생긴다. 예를 들면 사용자 user1, user2가 아이템에 내린 평점이 user1 = (1,1,1), user2 = (10,10,10) 라고 했을 때, 둘 사이의 코사인 유사도는 1이 된다. 예를 들면, 두 평점에 대한 유사도 $sim([1,1,1], [1,1,1])$과 $sim([1,1,1], [10,10,10])$ 의 결과는 1로 똑같이 나온다. 두 벡터는 완전히 상반된 선호도를 표시하고 있는데, 코사인 유사도는 완전히 같다는 결과를 낸다.
코사인 유사도는 다양한 차원이 존재할 때 유사도를 잘 나타낼 수 있는 장점도 있지만 앞서 말한 바와 같은 치명적인 단점이 존재한다.
동시 평가 항목이 1개인 경우 항상 1이 나온다는 점도 취약한 부분이다. 왜냐하면 1차원에서는 각을 고려할 수 없이 스칼라 값이 직선상에 놓이기 때문에 각이 0도가 나오기 때문이다.
정리하면 1. co-rated 아이템이 적은 경우 성능에 안좋은 영향을 미친다. 2. 값을 너무 높게 쳐주는 경향이 있다. 3. feedback 점수가 심각하게 차이가 있음에도 높은 유사도를 준다. [6] 덧붙이면 벡터가 가진 값의 크기보다 상대적인 값에 더 관심이 있는 경우 사용한다.
1.3 Adjusted Cosine Similarity(조정된 코사인 유사도)

조정된 유사도 같은 경우에는 아이템 간의 유사도를 구하는 과정에서 사용이 되고, 이 때 상관계수보다 일반적으로 나은 성능을 보인다고 한다. 그래서 인지 논문들을 찾아보다 보면 user 간 유사도 $sim(u,v)$ , $sim(u,v)$ , $sim(u,v)$ 하다가 조정된 유사도 설명이 나올때면 $sim(i,j)$ 처럼 아이템간의 유사도로 바뀌더라..
아무튼 문제점은 코사인 유사도, 상관계수와 유사하다. 먼저 유저 $u$가 동시 평가한 아이템(여기선 $i, i'$)이 적은 경우 성능에 악영향을 끼치며, 마찬가지로 평점의 상태가 심각히 다름에도 상당히 높거나 낮은 유사도 점수를 준다는 점이 있다.
1.4 Mean Squared Difference similarity(평균제곱차이 유사도)

MSD는 rating의 absolute 값을 고려한다. 유클리디안 거리를 구해 공통 평가 항목 수로 나눈 값을 1에서 빼줌으로써 1에 가까울수록 거리가 가까운 더 유사한 쌍을 나타내게 된다. MSD는 가장 큰 특징은 코사인 유사도에서는 할 수 없던 $r$이 가진 scale을 고려한다는 것이다. 이말은 곧 rating 의 정보를 얻을 수 있다는 것을 의미한다. 하지만 MSD 는 그 활용의 폭이 그리 넓지 않다. 또한 co-rated rating의 개수 비율에 대한 가중치를 줄 수 없다는 점과 rating벡터의 길이에 대해서 무시하게 되는 점(sim([1],[5]) = sim([1,1],[5,5]))도 존재한다.
1.5 Jaccard Similarity(자카드 유사도)

자카드 유사도는 대표적인 binary feedback에 대한 유사도를 측정할 수 있는 지표이다. 두 사용자 어느에게도 feedback이 없는 item은 제외한 상태에서 둘 사이의 유사도를 구한다. 위의 식 그대로 두 feedback 의 교집합을 합집합으로 나눈 값이다. sparse 한 행렬에서 기존의 co-occurrence(동시출현빈도)를 사용할 떄보다 유사도를 잘 표현해준다. 자카드 유사도의 장점은 co-rated 에 대해서 co-occurrence 를 고려하기 때문에 co-occurrence 에 대한 가중치를 잘 나타내줄 수 있다. co-rated 가 많을수록 더 similar 하다고 표현하는 지표이다.
1.6 단점(Drawbacks)
위의 정리한 유사도를 포함한 여러 유사도들의 단점을 정리한 표[8]는 아래와 같다.

우선 두 사용자가 유사함에도 불구하고 낮은 유사도를 내는 유사도 지표로는 PCC, SPCC, CPCC, ACOS 이 있다. 그리고 두 사용자가 유사하지 않고 전혀 다른 rating 분포를 가짐에도 높은 유사도를 내는 지표로는 SPCC, COS이 있다. MSD의 경우에는 co-rated rating의 비율을 무시하는 단점이 있고, 자카드 유사도의 경우 rating 값의 scale을 무시한다.
마지막으로 PIP, NHSM 은 아래의 논문[4]에 정리된 지표인데, 이 지표들은 높은 계산 복잡도와 복잡한 수식이라는 한계가 존재한다.
2. 사용자 피드백에 정성적 의미를 담기.
sparse 한 rating 행렬이 있다고 하자. 여기서 우리는 nan 이라는 sparse 한 값들을 마주하게 된다. 이 nan 값들은 행렬 대부분에 들어가있기 때문에 이에 대해서 0으로 처리를 한다거나, 평균값으로 대체하는 경우가 허다하다. 보통 평균으로 nan 값을 메꾸는 것이 더 성능이 좋다고는 한다.
이 장에서는 사실 sparse 한 문제를 해결하기 위한 직접적인 approach는 아니지만 rating 행렬에서 rated 된 값들이 가지는 의미를 수치적으로 나타내는 방법에 대해 알아본다. 내 생각엔 적은 rating 값들을 더 유의미한 값으로 만들어 활용하기 때문에 충분히 sparse 한 문제를 해결하는 방법 중에 하나라고 생각한다.
이에 [0]의 경우 아래와 같이 기존의 observed rating 을 변형한다.

위의 정의를 살펴보면, $pref_{>}(r_{ui})$ 는 $r_{ui}$ 가 사용자 $i$ 가 rate 한 특정 아이템에 대해 $i$ 가 rate 한 다른 아이템 $j$ 들에 매긴 rate 보다 높은 아이템의 개수를 말한다. $pref_{=}(r_{ui})$ 는 등호와 같이 다른 아이템들과 동일하게 매긴 개수를 의미한다. 첫번째 term 이 의미하는 것은 높은 점수를 주었을 때, 다른 아이템들과 비교하여 그 가치가 얼마나 더 큰 것인지를 나타내고, 두번째 term 같은 경우에는 전체적으로 점수의 폭이 얼마나 퍼져있는지 혹은 한 점수에 집중적인지를 나타내준다.
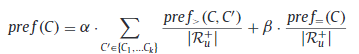
위의 정의를 살펴보면, $C$ 는 rating 을 할 수 있는 rating 값들의 집합이다. 평점이 1에서 5점까지 있다고 한다면, C={1, 2, 3, 4, 5} 이다. $\alpha$ 와 $\beta$ 는 hyperparameter로써 각 term에 비중을 얼마나 줄 것인지를 제어한다. 논문에서는 $\alpha$ 를 1.0, $\beta$ 를 0.5 로 두었다. 이말인 즉슨, 동일하게 평가한 아이템들이 많을 수록 $C$에 포함된 해당 점수에 대해 penalty를 주게 된다.
깊이 보지 않아서 자세히는 이해못했지만, 다만 사용자가 내린 평점 $r$에 각 사용자 별로 가중치를 다르게 준다는 것이 키포인트이다. 인상깊었다.
3. 유사도 변형을 통한 추천시스템 성능 향상 연구.
3.1 An improved collaborative recommendation algorithm based on optimized user similarity
[1]은 balancing factor 라는 것을 기존 전통적인 코사인 유사도 알고리즘에 추가한다. 코사인 유사도는 위에서 언급했든이 벡터가 가진 scale을 고려하지 않는다는 특징이 있었는데, 평점의 경우에는 사용자들의 single rating scale 이 중요하지 않을 수 없다.

위의 $sumDiffer(u_{a}, u_{b})$ 는 두 사용자 간의 오차제곱합의 평균이라고 생각하면 된다. MSE 같은 개념인데, 이를 활용하게 되면 평점이 가지는 scale을 위의 MSD가 가진 scale을 고려하는 특징을 사용할 수 있게 되는 것이다.
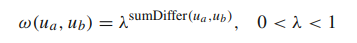
위와 같이 $sumDiffer(u_{a}, u_{b})$ 를 hyperparameter $\lambda$ 에 지수로 사용하여 $w(u_{a}, u_{b})$ 를 얻는다. 람다는 0과 1사이의 값이라 제곱할수록 값이 0에 가까워지게 되는데, $sumDiffer(u_{a}, u_{b})$ term 이 람다의 지수로 들어가기 때문에 작으면 작을 수록 좋다. 즉 오차가 작을 수록 가중치는 커지게 되는 결과를 얻게 된다.
마지막으로 구한 이 가중치를 아래와 같이 기존의 코사인 유사도에서 얻은 similarity에 곱한다.
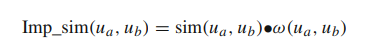
요약해보면, 기존의 코사인 유사도가 가지는 한계점을 scale을 고려할 수 있는 term 을 생성해 가중치로 사용하였다. 한계점을 잘 보완하였다.
3.2 Item-Based Collaborative Filtering with Attribute Correlation: A Case Study on Movie Recommendation
[2]는 Item 간의 유사도를 기반으로한 Item based collaborative filtering 알고리즘에서 아이템간의 유사도를 측정함에 있어서 장르, 감독 변수를 사용한다. 장르와 감독변수를 토대로 유사도를 구하는 방법은 아래와 같다.
Genre Correlation을 보면, $Sim(M_{i}, M_{j})$와 같다. 이는 영화 $i, j$ 사이의 similarity를 나타내는 지표이다.
MGC 장르간의 pearson correlation coefficient 중 최댓값을 사용한다. 두 영화 $i, j$ 가 가진 장르들을 하나씩 pairwise하게 PCC를 구해 최댓값을 사용한다. 그리고 MGN은 두 영화가 각각 가진 장르들중 최댓값을 선택한다.

아래는 감독간의 유사도를 구한다. 우선적으로 감독 x 장르 행렬을 구성한다. $M_{d}$ 는 감독 $d$ 가 만든 영화의 총 개수를 의미한다. $r_{d,g}$ 는 장르 $g$에서 감독 $d$ 의 비율을 의미한다. 즉 $d_{i,g}$ 는 감독이 한 장르에 대해 얼마나 많은 영화를 만들었는지로써 감독의 장르 성향을 나타낸다.

위에서 영화 장르 개수를 토대로 감독의 장르 성향을 구했다면, 이제 위의 구한 식을 토대로 아래와 같이 감독이 장르에 대해 가진 벡터로 코사인 유사도를 구한다.
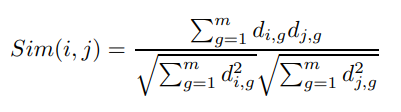
그리하여 위의 두 식을 결합한 아래와 같은 유사도를 생성하게 된다. $\beta$는 감독 유사도의 기여도에 대한 가중치이다.

이제 아래와 같은 item-based CF도 같이 수행해준다.

두 유사도를 합쳐주어 두 아이템 간의 유사도를 결정짓는다. 이 때 $\alpha$ 는 감독, 장르를 토대로 만든 유사도의 기여도에 대한 가중치 값이다.
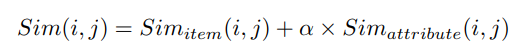
[2]에서는 $\alpha$ 와 $\beta$ 를 각각 0.4, 0.2를 두고 실험을 진행하였다.
최종적으로 아래와 같이 사용자 $u$가 $i$에 내릴 예측 평점은 가중평균을 통해 구하게 된다. 명시는 되어 있지 않지만 $N$은 사용자 $u$가 평점을 매긴 아이템들의 집합인 것 같다. 그리하여 $N$ 의 각 아이템과 $i$와의 유사도에 사용자가 내린 평점들의 가중평균으로 예측 평점이 계산된다.

movie lens 데이터셋을 토대로 장르, 감독, 시놉시스, 사용자 정보 등을 가지고 기존의 평점 매트릭스만 가지고 CF 를 했을 때 보다 좋은 성능을 내는 연구결과는 많다. 이 논문의 경우에는 직관적으로 감독과 장르간의 유사도를 구한 점과 $\alpha, \beta$를 넣어 term의 영향력을 조절해주는 부분이 인상깊었다.
3.3 A new collaborative filtering metric that improves the behavior of recommender systems
[3]은 자카드 유사도에 MSD 유사도를 곱한 값을 사용한다. 자카드 유사도의 특징인 co-rated 에 대한 가중치를 부여하며 rating vector가 가진 값들의 scale을 고려하는 MSD 유사도의 특징을 결합한 것이라고 할 수 있다.
아래와 같이 x, y두 rating 벡터가 있을 때, 두 벡터의 co-rated 평점이 많을 수록, 두 벡터의 각 값에 대한 오차가 적을수록 newmetric(x,y)의 유사도는 높은 점수를 얻게 된다.

[1] 에서 자카드 유사도에 error 값을 사용하는 term 을 추가하는 반면 이 논문에서는 다이렉트하게 두 유사도를 곱해버리는 직관적인 유사도 지표를 제시하여 인상 깊었다.
3.4 A new user similarity model to improve the accuracy of collaborative filtering
[4]는 평점이 가지는 상대적인 의미를 다양하게 고려하여 조합하는 새로운 유사도 측정 모형을 만들어냈다. 아래의 $sim(u,v)^{NHSM}$ 는 제안한 유사도 지표이며, NHSM 은 New Heuristic Similarity Model 의 약자이다.
$sim(u,v)^{NHSM}$ 는 $sim(u,v)^{JPSS}$와 $sim(u,v)^{URP}$의 곱으로 구한다.
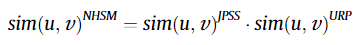
먼저 $sim(u,v)^{JPSS}$ 부터 살펴보도록 하자.
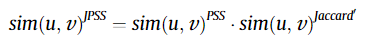
JPSS 유사도는 자카드 유사도와 PSS 유사도를 곱한 것이다. 자카드 유사도는 이미 알고 있는 자카드 유사도가 맞으며 PSS 유사도는 아래와 같다.


PSS 유사도 같은 경우에는 아래와 같이 세가지 특징을 결합한 형태이다.
Proximity는 두 사용자가 매긴 평점의 차이에 대한 정보를 활용한다. 즉 평점의 scale을 반영한다고 할 수 있다. 그 term 은 $|r_{u,p}-r_{v,p}|$ 에 해당한다.
Significance는 특정 사용자가 매긴 하나의 평점이 사용자가 내린 평점들에 비해 상대적으로 의미있는 평점인가를 나타낸다. 아래의 식을 보면 해당 아이템의 평점의 중앙값(median)을 빼줌으로써 중앙으로부터 멀수록 그 평점은 더 중요한 정보를 가진다고 평가한다. 그 term은 $|r_{u,p}-r_{med}| \cdot |r_{v,p}-r_{med}|$ 이다.
Singularity는 두 평점이 다른 평점들과 비교해서 얼마나 다른지를 나타낸다. 아래의 term은 $| \frac{r_{u,p}+r_{v,p}}{2} - \mu_{p}|$ 으로써 두 평점의 평균이 아이템 $p$의 평균과 얼마나 차이가 나는지를 나타냄으로써 이 두 평점의 Singularity를 측정한다.
Proximity, Significance, Singularity는 각각 시그모이드 함수를 거쳐 0~1 사이의 값으로 매핑하게 한다.

Proximity, Significance, Singularity 를 모두 곱해서 아래와 같이 하나의 값으로 만든다.
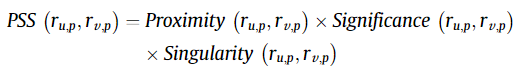
이제 $sim(u,v)^{URP}$ 에 대해 알아보자.
각 유저의 성향을 고려한다. 각 사용자는 각기 다른 평점 성향을 지닌다. 어떤 사용자는 높은 평점을 주며, 어떤 사용자는 낮은 평점을 주는 성향이 그 예이다. 이러한 사용자들의 성향을 반영하기 위하여 평점의 평균과 분산을 활용한다. 이를 활용한 식은 아래와 같다. 그 term이 $|\mu_{u} - \mu_{v}| \cdot |\sigma_{u} - \sigma_{v}|$ 이다. 각 평균의 차가 크다는 것은 두 사용자의 평균적으로 매긴 평점들이 그만큼 다르다는 것이다. 각 표준편차 $\sigma$ 의 차이가 클수록 두 사용자의 분산도 그만큼 차이가 나는 것이다.
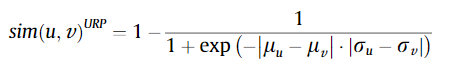
최종적으로 $sim(u,v)^{JPSS}$와 $sim(u,v)^{URP}$ 의 유사도를 구했으니 모두 곱하기만 하면 최종적으로 $sim(u,v)^{NHSM}$ 유사도를 얻게 된다. 이 유사도를 이제 user-based CF 알고리즘의 유사도 부분에 사용하면 된다.
두 사용자의 평점이 주는 의미를 수식으로 표현하므로써 상대적 의미를 잘 표현한 것 같다. 개인적인 생각으로는 $sim(u,v)^{URP}$ 에서 평균이 동일하거나 분산이 동일한 경우에는 $sim(u,v)^{URP}$가 바로 0으로 수렴해버리는 현상을 좀 손보고 싶다는 생각이 들었다. 실제로 평균이 동일하거나 분산이 동일한 경우는 적긴 하지만 말이다..
3.5 An improved collaborative filtering method based on similarity
[5] 는 [4]논문을 참조해서 그 유사도 구하는 과정에서 참조하면서 낸 논문으로 보인다. 아래와 같이 $Sim(u,v)^{Proposed}$ 는 세가지 유사도를 곱한 값으로 구해지는데, 하나씩 살펴보도록 하자.
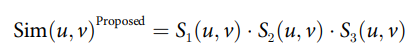
$S_{1}$ 은 아래와 같다. 부피가 커서 많아보이기는 하지만 사실상 큰 의미는 없다.
먼저 강조하고자 하는 부분은 sparsity를 연구자가 지정한 임계치 $\rho$ 보다 작은 경우에는(sparse 하다.) 기존의 코사인 유사도를 구하듯이 구하지만, 분모를 보면 알겠지만, 공통 평점 집합이 아니라 각각 평가한 평점들에 대한 norm2를 구해서 곱하는 것을 알 수 있다. 즉 한 사용자가 매긴 평점 모두를 사용하겠다는 것이다.
임계치보다 큰 경우에(sparse 하지 않다.) 대해서는 co-rated 평점만 사용하는 것이 아닌 두 사용자가 매긴 평점들을 모두 활용하는 것이다. unrated item에 대해선 평균값으로 대체하였다. 그렇기 때문에 이 연산이 가능해지게 된다.

$S_{2}(u,v)$ 는 아래와 같다. 이 term이 말하고자 하는 것은 동시 평가된 항목들이 많을수록 더 중요하다고 판단, 동시 평가 항목의 비율이 클수록 $S_{2}(u,v)$의 값도 커진다. 시그모이드 input $x$ 에 들어간 term을 보면 co-rated 평점 개수를 제곱한 값을 각 평점 개수 곱한 것으로 나눈다. 이말인 즉슨 동시 평가한 항목에 제곱을 줌으로써 그 가중치를 많이 주겠다는 의미이다.
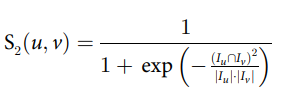
$S_{3}(u,v)$의 경우에는 [4] 논문에서 제시한 것과 동일하므로 생략한다.

아무튼 세개의 term을 곱해서 유사도를 생성하고, 마찬가지로 user-based CF 알고리즘에 유사도로 사용하여 예측평점을 뽑아내게 된다.
요약하면 "최대한 많은 평점자료"를 , "동시 평가 항목의 개수"의 중요성을, "두 사용자의 평점 성향"을 반영하였다.
3.6 An efficient recommdation generation using relevant Jaccard similarity.
[7] 은 [3]에서 자카드 유사도와 MSD 유사도를 곱한 유사도를 구하는 것과 비슷하다. 다만 자카드 유사도의 형태를 변형하였다. 아래의 식에서 $Sim(u,v)^{RJaccard}$부분이 바로 그 부분이다. 이 유사도 $Sim(u,v)^{RJaccard}$에 대해서 살펴보자.


우선 $|\bar{I}_{u}|$ 는 un-co-rated 평점으로써 사용자 $u$가 평가한 것 중 동시 평가 항목이 아닌 것에 해당한다. 그러므로 기존의 자카드 유사도가 아래와 같다고 할 때,

아래와 같이 전개될 수 있다. 가장 오른쪽에 분모 부분을 보면, 쉽게 이해가 가능하다. 결과적으로 분모부분은 합집합을 나타낸다.

이제 아래와 같이 변형을 할 수 있다. 분자와 분모에 교집합 term으로 나누어 전개한 것이다. 지금까지는 계속 같은 식을 모양만 바꾸고 있는 것이다.
아래의 식이 표현하고 있는 것은 자카드 유사도는 co-rated 평점개수와 비례한다는 점과 $|\bar{I}_{u}|$ + $|\bar{I}_{v}|$ 의 역수인 $(|\bar{I}_{u}| + |\bar{I}_{v}|)^{-1}$ 와 비례한다는 것이다.
.

[7]은 $(|\bar{I}_{u}| + |\bar{I}_{v}|)^{-1}$ term이 적절한 추천을 하는데 있어서 자카드 유사도에서 부적절한 역할을 한다고 말한다. 자카드 유사도는 최소의 co-rated 평점을 활용하여 inadequacy와 improvement를 얻는다. 하지만 사용자가 매우 유사할 때는 오직 co-rated에 대해서만 그런 것이다. 그러므로 평점을 예측할 때 유사한 사용자는 필요가 없다. 아래의 예시를 보면 더 쉽게 이해를 할 수 있다.


Table 1은 target user $U_{1}$ 에 대해서 nearest neighbors 들과 비교했을 때, $U_{1}$이 매기지 않은 것에 대해서 이웃들이 각각이 평가한 항목이 몇 개인지를 카운트한 표이다. Table 2는 $U_{1}$이 평가한 항목들 중에서 이웃들은 평가하지 않은 항목의 개수를 카운트한 표이다. '-' 표시는 missing rating을 뜻한다.
Table1에서 $U_{1}$과 $U_{2},U_{3},U_{4}$와 가장 유사하다고 볼 수 있다. 왜냐하면 $U_{1}$가 평가한 평점들에 대해서 $U_{2},U_{3},U_{4}$는 모두 평가를 했기 때문이다. 하지만 $I_{2}$와 $I_{5}$에 대해서는 $U_{2},U_{3},U_{4}$는 역시 평가를 하지 않았기 때문에 이러한 사용자는 평점을 예측하는데 쓸모가 없어진다. 하지만 $U_{5},U_{6}$ 사용자의 경우에는 $U_{2},U_{3},U_{4}$ 사용자보다는 상대적으로 덜 유사하지만 그래도 $I_{2}, I_{5}$를 평가했기 때문에 평점 예측에 효율적이다. 그래서 이 아이디어는 자카드 유사도는 사용자 $u$는 특정 항목에 평가하지 않았지만 $v$는 평가한 개수를 나타내는 $|\bar{I_{v}}|$ term과 비례한다는 것을 말한다.
이어서 Table2에서는 $U_{1}$ 은 $U_{2},U_{3},U_{4}$와 유사도를 구할 때 오직 한개의 아이템으로만 계산이 된다. 반면에 $U_{5}, U_{6}$ 는 각각 5개, 4개의 co-rated를 가지고 유사도를 구하게 된다. 이는 $U_{1}$ 과 $U_{5},U_{6}$는 적절한 유사도를 측정할 수 있다는 것을 의미한다. 그래서 이 아이디어는 자카드 유사도는 사용자 $u$는 특정 항목에 평가했지만 $v$는 평가하지 않은 개수를 나타내는 $|\bar{I_{u}}|$ term과 반비례한다는 것을 말한다.
기존의 CF 알고리즘의 경우는 유사도를 구할 때 극단적인 이웃들을 활용하게 된다. Table1, Table2로 설명했더 것들을 고려하지 않았다는 말이다. 그렇기 때문에 효과적인 이웃을 찾는다거나 평점 예측에 있어서 불충분했다고 할 수 있다. 이에 새로운 자카드 유사도 지표를 제시한다.
.



위의 아이디어를 녹여낸 최종 변형된 자카드 유사도 식은 아래와 같다.


분모에 term 들에서는 분모가 클수록 자카드 유사도와 비례하여 값이 커진다는 것에 유의하며 살펴보자. 우선 $\frac{1}{|I_{u} \cap I_{v}|}$는 동시 평가 항목이 많을 수록 유사도가 높다고 표현하는 term 이다. 그리고 $\frac{|\bar{I_{u}}|}{1+|\bar{I_{u}}|}$는 $u$만 평가한 항목이 많을 수록 반비례한다는 term이다. 마지막으로 $\frac{1}{1+|\bar{I_{v}}|}$는 $v$만 평가한 항목이 많을수록 높은 점수를 주는 term 이다.
이논문은 직접 유사도를 계산하는 과정을 실제 데이터로 들여다보거나 EDA를 하지 않으면 얻어낼 수 없는 아이디어이다. CF알고리즘을 구현하여 유사도를 구하는 것을 해본 사람이라면 누구나 공감하는 문제이다. 동시 평가 항목이 극히 적거나, 유사한 이웃인데 예측평점에 만들 항목에는 평가를 하지 않아서 추천에 사용될 수 없는 경우 등등.. 이 문제를 논리적으로 잘 구성한 연구였다고 생각한다.
Sparsity 문제에서 주어진 정보를 최대한 의미있게 사용하는 이 연구분야는 꽤 매력있는 분야인 것 같다.
ref)
[0] Improving the accuracy of top-N recommendation using a preference model(2016)
[1] An improved collaborative recommendation algorithm based on optimized user similarity(2016)
[2] Item-Based Collaborative Filtering with Attribute Correlation: A Case Study on Movie Recommendation(2014)
[3] A new collaborative filtering metric that improves the behavior of recommender systems(2010)
[4] A new user similarity model to improve the accuracy of collaborativefiltering(2014)
[5] An improved collaborative filtering method based on similarity(2018)
[6] A New Similarity Measure Based on Mean Measure of Divergence for Collaborative Filtering in Sparse Environment(2016)
[7] An efficient recommendation generation using relevant Jaccard similarity(2019)
[8] A new similarity measure for collaborative filtering based recommender systems(2019)
'추천시스템' 카테고리의 다른 글
| Collaborative Filtering 에서의 유사도 지표 제안 논문(2). (0) | 2020.11.09 |
|---|---|
| Collaborative Filtering 에서의 유사도 지표 제안 논문. (0) | 2020.10.29 |
| 메모리 기반 CF 추천시스템의 문제점 (0) | 2020.08.23 |
| SVD 를 활용한 협업필터링 (4) | 2020.02.22 |
| surprise를 활용한 협업필터링(collaborative filtering) (3) | 2020.02.13 |



댓글