협업필터링은 메모리 기반과 모델 기반으로 나뉜다고 했다. 근데 여기서 모델기반 중 클러스터링 기법, 행렬 축소 기법, 딥러닝 기법이 있는데 이번 장에서는 행렬 축소 기법 중 하나인 SVD(특잇값 분해: Singular Vector Decomposition)에 대하여 간단히 알아보고, MovieLens데이터를 SVD를 활용하여 추천을 하는 코딩을 해보도록 하였다.
https://drive.google.com/drive/folders/1EwDW7RMbJrKvvDdZCHWpFpQ2gbmpj1Y9?usp=sharing
위의 링크를 타면 사용중인 movielens 데이터를 txt형태로 받을 수 있따.
1. SVD란
SVD는 Latent Semantic Indexing의 부분으로써, 동의어나 다의어로부터 오는 문제를 해결하기 위해 정보 검색 분야에 널리 사용되고 있다. 추천 분야에서 SVD는 거대한 행렬을 축소시킬 수 있고, 축소된 행렬에서 확연히 줄어든 계산량으로 사용자 또는 아이템 간의 유사도를 구할 수 있게 해준다. 결과부터 말하면 계산량도 줄고, 정확도는 기본적인 협업필터링보다야 낫다. 하지만 해석에 있어서 그 요소들을 설명하기 까다로워지는 단점이 있긴하다.
$A = U\sum V^{T}$
위의 특잇값분해 형태를 쉽게 설명하면 A라는 행렬을 $U$, $\sum$, $V^{T}$ 세 행렬의 행렬곱으로 나타내는 것이다. 이를 대각화라고 하며, 고윳값 분해에서 정방행렬에 대해서만 대각화를 할 수 있었던 것과는 달리 특잇값분해에서는 모든 $m x n$ 행렬에 대해서 적용이 가능하다.
가운데 $\sum$를 특잇값(singular vector)이라 하고, $U$와 $V^{T}$를 각각 left singular vector, right singular vector라고 한다.
아래의 그림은 이해를 돕기 위해 참조[3]을 통해 스크랩하였다.
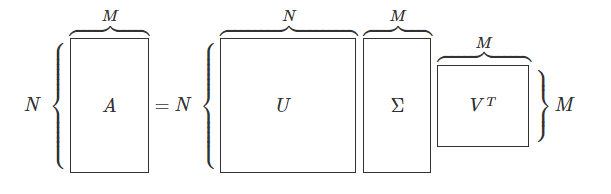

영화 평점 데이터 MovieLens를 사용했을 때, 사용자-아이템 평점 행렬을 $사용자 행렬 \times 특잇값 행렬 \times 영화 행렬$ 로 만들어 축소된 데이터를 활용하여 해당 사용자가 평가하지 않은 영화에 대한 평점을 예측하여 채워넣는 방식으로 진행한다.
2. SVD를 통한 협업필터링 과정
[1]에 나와 있는 "The Algorithm: Item-based Filtering Enhanced by SVD" 순서를 그대로 번역하면 아래와 같다.
1. 아이템 $n$에 대한 사용자 $m$들의 평점을 가진 행렬 $m \times n$ 을 정의한다. $r_{ij}$는 아이템 $i_{j}$ 에 대한 사용자 $u_{i}$의 평가를 나타낸다.
2. 모든 결측값을 제거하기 위해 사용자-아이템 행렬 $R$을 전처리 한다. 전처리는 다음과 같다.
(a) 행렬 $R$로 부터 모든 행의 평균 $r_{i}$을 구하고 모든 열의 평균 계산한다. 마찬가지로 모든 열에 대한 평균 $r_{j}$를 구한다.
(b) 전체 행렬 중 결측값에 해당하는 엔트리에 해당 컬럼에서 구한 평균 값인 $r_{j}$를 입력하여 이 행렬을 $R_{filled-in}$ 이라 명시합니다.
(c) $R_{filled-in}$ 행렬에 전부 행의 평균 $r_{i}$을 빼줌으로써 정규화된 행렬 $R_{norm}$을 얻는다.
3. 앞서 만든 행렬을 특잇값 분해(SVD) 하여 다음 처럼 만든다. $R_{norm} = U \cdot S \cdot V^{T}$ .
4. 차원 축소 단계를 진행하는데, $k$ 대각 원소를 가진 $S$ $(k \times k)$ 행렬을 가져오면서 $U$와 $V^{T}$ 도 각각$(m \times k)$ , $(k \times n)$으로 만든다.
이 때, 축소된 행렬 $R_{red}$는 다음과 같이 나타낸다. $R_{red} = U_{k} \cdot S_{k} \cdot V_{k}^{T}$
그리고 이 축소된 행렬에서 $rr_{ij}$는 사용자 $u_{i}$가 아이템 $i_{j}$에 평가한 것을 나타낸다.
5. $\sqrt{S_{k}}$를 계산하고, 두 행렬과의 행렬곱을 수행한다. $U_{k} \cdot \sqrt{S_{k}}^{T}$는 사용자 $m$을 나타내고, $\sqrt{S_{k}} \cdot V_{k}^{T}$ 는 아이템 $n$을 나타내고, 이들은 각각 $k$ 차원 특징 공간안에 존재한다. 특히 후자의 행렬 $(k \times n)$에 관심이 있다. 왜냐하면 아이템 $n$에 대한 pseudo-사용자에 의해 제공된 "메타" 평점을 나타내기 때문이다. pseudo-사용자 $u_{i}$가 아이템 $i_{j}$에 할당한 "메타" 평점을 $mr_{ij}$라 표기한다.
6. 두가지 서브 스텝으로 쪼개진 이웃 형성 단계를 진행한다.
(a) 아이템 $i_{j}$와 $i_{f}$ 간의 유사도를 조정된 코사인 유사도를 사용하여 구한다.
$sim_{jf} = adjcorr_{jf} = \frac{\sum_{i=1}^{k} mr_{ij} \cdot mr_{if}}{\sqrt{\sum_{i=1}^{k} mr_{ij}^{2} \cdot \sum_{i=1}^{k} mr_{if}^{2}}}$
$k$는 차원 축소 단계에서 선택된 pseudo-사용자들의 수 이다. 일반적인 아이템 기반 필터링에서 개별 사용자 간의 등급 척도 차이는 각 공동 등급(동시평가된) 아이템 쌍에서 해당 사용자의 평균을 뺀 값으로 상쇄되었다. SVD 기반 아이템 기반 필터링에서 등급 척도의 차이는 행렬 $R_{norm}$을 산출한 원래의 사용자-아이템 행렬의 정규화 수행 중에 상쇄된다.
(b) 해당 아이템과 한 랜덤 아이템을 포함한 아이템 쌍들에 대한 조정된 코사인 유사도 계산 결과를 바탕으로 해당 아이템과 가장 유사한 것으로 보이는 아이템들의 집합을 분리시켜준다.
7. 다음의 가중 합으로 예측치를 생성한다. 이는 아이템 $i_{j}$에 대한 사용자 $u_{a}$에 대한 예측치를 계산하는 것을 말한다.
$pr_{aj} = \frac{ \sum_{k=1}^{l} sim_{jk} \cdot (rr_{ak} + \bar{r}_{a})}{\sum_{k=1}^{l} |sim_{jk}|}$
해당 아이템 $i_{j}$와 가장 유사한 것으로 선택된 $l$ 아이템들에 대해 해당 사용자가 평가한 등급에 대한 예측을 기반으로 한다는 점에서 일반적인 아이템 기반 필터링과 사용하는 방정식이 유사하다.
그러나, 사용자 등급이 축소된 사용자-아이템 행렬 $R_{red}$에서 가져온다는 것이 다르다. 또한 정규화 전처리 단계에서 뺐던 사용자 평균 $\bar{r}_{a}$를 다시 더해주어야 한다.
3. 코드 구현
MovieLens 데이터를 불러오고 간단한 전처리를 한 후 피벗테이블까지 만든다.
아래의 사이트에서 데이터를 수집한다. 가장 작은 분석용 데이터인 'older datasets'를 다운 받았다.
https://grouplens.org/datasets/movielens/
MovieLens
GroupLens Research has collected and made available rating data sets from the MovieLens web site ( The data sets were collected over various periods of time, depending on the size of the set. …
grouplens.org
import pandas as pd
import numpy as np
import math
#데이터 불러오기
ratings = pd.read_csv("u.data.txt", header=None, sep='\t')
#컬럼명 수정
ratings.columns = ['userid','movieid','rating','timestamp']
#불필요한 컬럼 제거
ratings = ratings.drop(['timestamp'], axis=1)
#피벗테이블로 만들어서 사용자-아이템 행렬 확인하기
rating_table= pd.pivot_table(ratings, values='rating', index=['userid'], columns=['movieid'])
rating_table
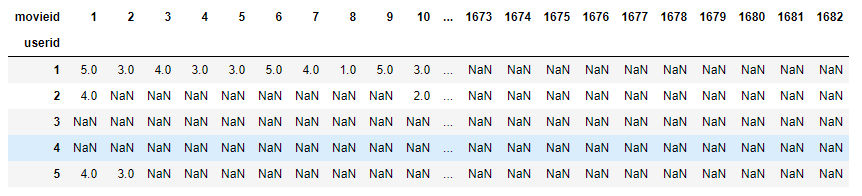
사용자-아이템 행렬 $R$을 정의하였다. 이제 앞서 본 논문의 순서대로 진행해보도록 한다. 1번은 진행하였으니 바로 2번으로 넘어간다.
2번은 NaN에 컬럼별 평균값을 컬럼에 맞게 채워준다. 그렇게 $R_{filled-in}$ 행렬을 만들어 준다. 그리고 $R_{filled-in}$행렬에서 모든 값에 대해서 해당 행의 평균을 빼준다.
def R_filled_in(rating_table):
for col in range(len(rating_table.columns)):
col_update=[]
# 컬럼의 평균을 구한다.
col_num = [i for i in rating_table.iloc[:,col] if math.isnan(i)==False]
col_mean = sum(col_num)/len(col_num)
# NaN을 가진 행은 위에서 구한 평균 값으로 채워준다.
col_update = [i if math.isnan(i)==False else col_mean for i in rating_table.iloc[:,col]]
# 리스트로 만든 업데이트된 한 컬럼을 기존에 데이터 프레임 컬럼에 새로 입혀준다.
rating_table.iloc[:,col] = col_update
return rating_table
rating_R_filled = R_filled_in(rating_table)
rating_R_filled
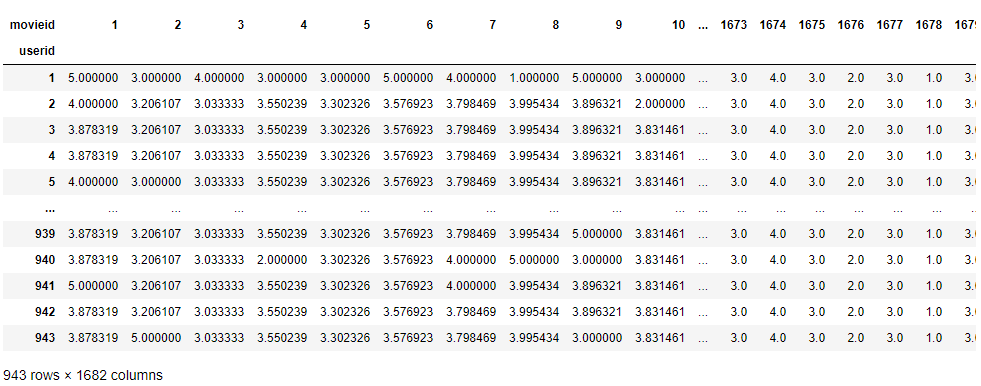
NaN 이었던 곳은 각 해당 컬럼의 평균값으로 대체된 것을 확인했다. 이제 모든 슬롯에 대해 해당 행의 평균값을 빼준다.
def R_norm(rating_R_filled):
for row in range(len(rating_R_filled)):
# 각 값에 평균을 빼준 값들을 넣을 리스트 공간 생성.
row_update=[]
# 행 평균 값
row_mean=sum(rating_R_filled.iloc[row,:])/len(rating_R_filled.iloc[row,:])
# 해당 행의 모든 컬럼 값에 행 평균 값을 뺀다.
row_update= [i-row_mean for i in rating_R_filled.iloc[row,:]]
rating_R_filled.iloc[row,:] = row_update
return rating_R_filledR_norm(rating_R_filled)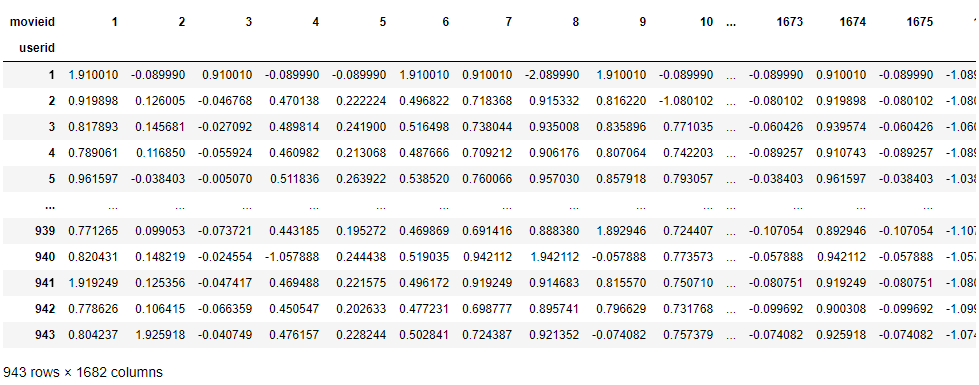
이로써 2번까지 완료하였다. 이제부터가 중요하다. 바로 이 행렬 $R_{norm}$을 특잇값분해하는 과정이다.
3번을 수행하기 위해 k 요소를 추출하여 행렬을 축소시키는 truncated SVD를 지원하는 sklearn.decomposition라이브러리의 TruncatedSVD를 활용한다. 이 메소드에 대한 자세한 설명은 아래의 사이트에 나와있다.
https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.TruncatedSVD.html
sklearn.decomposition.TruncatedSVD — scikit-learn 0.22.1 documentation
scikit-learn.org
from sklearn.decomposition import TruncatedSVD
# TruncatedSVD를 사용해서 차원축소를 해보자. 여기서 k는 12로 두었다. n_iter는 랜덤 SVD 계산기의 반복횟수이다.
svd = TruncatedSVD(n_components=12, n_iter=5)
# 모델을 데이터에 맞추는 작업
svd.fit(np.array(rating_R_norm))
# 다음의 코드를 통해 각각 행렬 U, S, V^T 를 변수에 담아낼 수 있다.
U=svd.fit_transform(np.array(rating_R_norm))
Sigma=svd.explained_variance_ratio_
VT= svd.components_

이미 SVD를 다 계산해주기 때문에 어렵지 않게 수행할 수 있었다. $k$를 12로 두어 요소를 다 추출해냈으니 4번까지는 다 진행한 셈이다.
이제 5번을 수행한다. $S_{k}$는 루트를 씌워준다. 그런뒤 $U_{k} \cdot \sqrt{S_{k}}^{T}$ 와 $\sqrt{S_{k}} \cdot V_{k}^{T}$ 행렬을 각각 만들어 준다.
# 시그마 행렬에 요소들에 루트를 씌워주는 작업.
Sigma_sqrt=[]
for i in range(len(Sigma)):
tmp=[]
tmp=[math.sqrt(s) for s in np.diag(Sigma)[i]]
Sigma_sqrt.append(tmp)
Sigma_sqrt=np.array(Sigma_sqrt)
# 행렬 곱
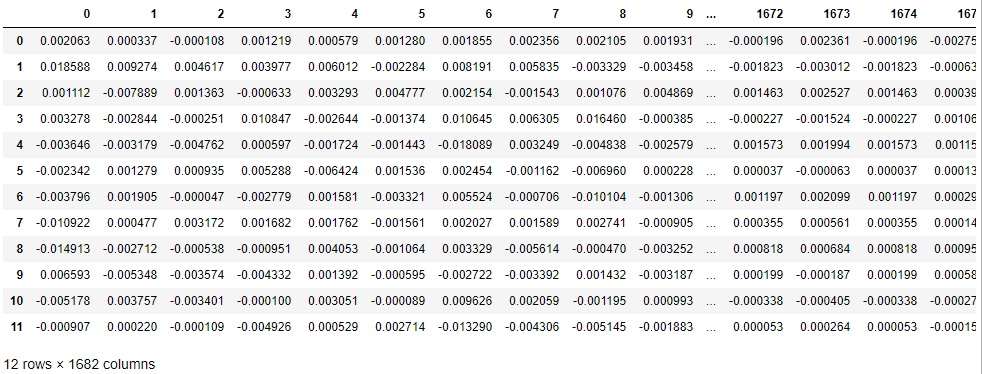
pd.DataFrame(np.matmul(U, Sigma_sqrt))$U_{k} \cdot \sqrt{S_{k}}^{T}$ 행렬. 이 행렬은 $m$ 사용자에 대한 특징이 12인 행렬이다.

# 행렬곱
pd.DataFrame(np.matmul(Sigma_sqrt, VT))$\sqrt{S_{k}} \cdot V_{k}^{T}$ 행렬. 이 행렬은 $n$ 아이템에 대한 특징이 12인 행렬이다.
이제 세 행렬을 행렬곱을 통해서 하나의 유사 행렬로 만들어준다. $R_{red}$.
#행렬곱
ratings_reduced= pd.DataFrame(np.matmul(np.matmul(U, np.diag(Sigma)), VT))
ratings_reduced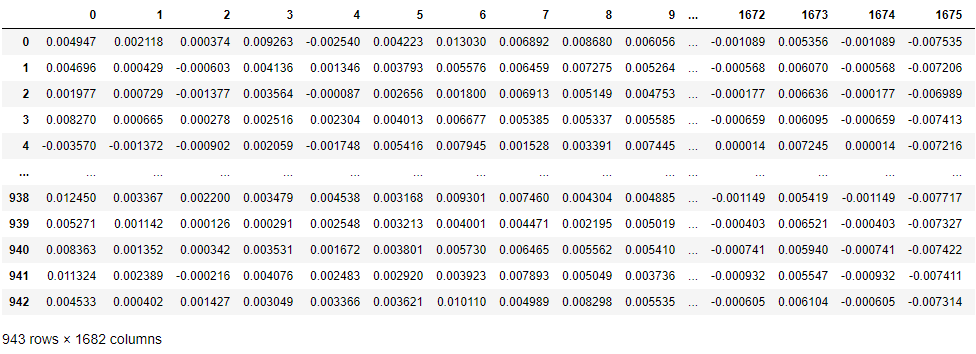
만들어진 $R_{red}$은 기존은 행렬 $R$의 근사한 행렬이므로 모든 빵꾸를 매꿨기에 여기다가 빼준 $R$에서 구한 사용자 별 평균을 다시 더해주면, 그대로도 추천이 가능하다.
하지만 이번 장에서는 논문에 나온 공식을 고대로 사용할 것이기 때문에 7번에 나온 공식을 활용해서 최종적으로 추천을 하도록 한다. 유사도는 5번에서 구한 $\sqrt{S_{k}} \cdot V_{k}^{T}$ 에서 구한다.
아이템 기반 협업필터링과 방법을 거의 나란히 하고 있다. 즉, 예측하려는 아이템 $j$와 pseudo-사용자가 평가한 아이템 간의 유사도를 구해서 상위 $k$를 사용해서 구한다.
깔끔하게 코드를 정리하여 최종 추천까지 진행해보자.
1. 데이터 불러와서 피벗테이블로 만들기.
import pandas as pd
import numpy as np
import math
ratings = pd.read_csv("u.data.txt", header=None, sep='\t')
ratings.columns = ['userid','movieid','rating','timestamp']
ratings = ratings[['userid','movieid','rating']]
rating_table= pd.pivot_table(ratings, values='rating', index=['userid'], columns=['movieid'])
2. 각 행, 열 별로 평균 값 구하기
row_mean= list(rating_table.mean(axis=1))
col_mean= list(rating_table.mean())
2.1. $R_{filled-in}$ 행렬 만들기.
def R_filled_in(rating_table, col_mean):
result= rating_table
for col in range(len(result.columns)):
col_values= list(result.iloc[:,col])
result.iloc[:,col]=[i if math.isnan(i) == False else col_mean[col] for i in col_values]
return resultR_filled_in = R_filled_in(rating_table, col_mean)
3. $R_{norm}$ 행렬만들기
def R_norm(R_filled_in, row_mean):
result = R_filled_in
for i in range(len(row_mean)):
result.iloc[i,:] = [v-row_mean[i] for v in result.iloc[i,:]]
return result
R_norm = R_norm(R_filled_in, row_mean)
4. SVD행렬과 유사도 계산을 위한 $\sqrt{S_{k}} \cdot V_{k}^{T}$ 행렬 구하기.
from sklearn.decomposition import TruncatedSVD
def SVD(R_norm, k = 12, n = 5):
# svd를 위한 라이브러리
from sklearn.decomposition import TruncatedSVD
# 요인을 12로 두고 계산반복을 5회로 하여 진행
svd = TruncatedSVD(n_components=k, n_iter=n)
svd.fit(np.array(R_norm))
U=svd.fit_transform(np.array(R_norm))
Sigma=svd.explained_variance_ratio_
VT= svd.components_
#행렬곱으로 R 행렬과 근사한 행렬을 생성
ratings_reduced= pd.DataFrame(np.matmul(np.matmul(U, np.diag(Sigma)), VT))
# 유사도를 구하기 위한 행렬
Sigma_sqrt=[]
for i in range(len(Sigma)):
tmp=[]
tmp=[math.sqrt(s) for s in np.diag(Sigma)[i]]
Sigma_sqrt.append(tmp)
# m 아이템 행렬 생성
sqrt_Sigma_mul_VT = pd.DataFrame(np.matmul(Sigma_sqrt, VT))
return ratings_reduced, sqrt_Sigma_mul_VTR_reduced, sqrt_S_VT=SVD(R_norm)
5. 코사인 유사도 함수 만들기.
def cos_sim(x,y): #x,y는 리스트형태 벡터.
x_2 = math.sqrt(sum([pow(i,2) for i in x]))
y_2 = math.sqrt(sum([pow(i,2) for i in y]))
multi= sum([i*j for i,j in zip(x, y)])
return multi / (x_2 * y_2)
6. 이제 전혀 sparsity 하지 않은 행렬이 있기 때문에 모든 사용자에 대한 예측 평점을 구할 수 있다.
예측 평점 매트릭스를 계산한 후, 사용자가 과거에 평가했던 아이템을 제외한 나머지 아이템들에 대해 예측 평점이 높은 것부터 추천해주면 된다.
주의할 점은 아이템 간의 유사도는 메타행렬로 부터 구해야한다는점과 이웃을 논문 결과를 토대로 10으로 설정하였기 때문에 각 예측평점을 구할 때 분모분자에 $\sum$을 $\sum_{k=1}^{10}$ 로 하여 계산해야한다.
pred_matrix = []
for a in range(len(R_reduced.index)): # 모든 활성 사용자 루프
K = list(ratings[ratings['userid']==a+1]['movieid'])
a_j_pred=[]
for j in range(len(R_reduced.columns)): # 모든 아이템 루프
sim_basket = []
for k in K: # 활성사용자가 평가한 아이템 루프
j_k_sim = cos_sim(sqrt_S_VT.iloc[:,j], sqrt_S_VT.iloc[:,k-1])
sim_basket.append([k, j_k_sim])
# 자기자신은 제외하고 10개를 선택함.
top_k= pd.DataFrame(sim_basket,columns=['k','similarity']).sort_values('similarity',ascending=False).head(11).reset_index().iloc[1:,:]
#분모
sum_sim = sum([np.abs(i) for i in list(top_k.loc[:,'similarity'])])
#분자
sum_up = []
for kk in list(top_k.loc[:,'k']):
sum_up.append(float(top_k[top_k['k']==kk]['similarity'] * (R_reduced.iloc[a,j-1] + row_mean[a-1])))
print('활성사용자 ',a,'의 ',j ,'아이템 평점 계산' )
a_j_pred.append((sum(sum_up)/sum_sim))
pred_matrix.append(a_j_pred)
pred_result = pd.DataFrame(pred_matrix)
pred_result.to_excel('SVD_recommendation.xlsx')시간이 너무 오래걸려서 바로 엑셀로 저장하게 하였다.
저장한 예측 평점 행렬 엑셀 파일을 다시 불러와서 활성사용자에 대한 추천을 해보도록 한다.
import pandas as pd
# 엑셀 불러오기
pred = pd.read_excel('SVD_recommendation.xlsx', header=0)
# 필요없는 첫 행(인덱스) 제거
pred.drop([pred.columns[0]],axis=1, inplace=True)
영화 데이터 불러오기
movies = pd.read_csv("u.item.txt", header=None, sep='|')
장르에 대한 정보를 만들어 준다.
fields=['movieid','movie title','release date','video release date','IMDb URL','unknown','Action','Adventure','Animation','''Children's''','Comedy','Crime','Documentary','Drama','Fantasy','Film-Noir','Horror','Musical','Mystery','Romance','Sci-Fi','Thriller','War','Western']
genre=[]
c=list(movies.columns)
c=c[6:]
for row in range(len(movies)):
genre_tmp=[]
for g in c:
if movies.loc[row, g] == 1:
genre_tmp.append(fields[g])
else:
continue
genre.append(' / '.join(genre_tmp))movies=movies.iloc[:,[0,1]]
movies.columns = ['movieid','movie title']
movies['genre']=genre
movies.head()
전처리를 하고 item데이터와 예측 평점 데이터를 활용하여 특정 사용자에 대한 추천 리스트를 top개 만큼 뽑는다.
def rec(user, top):
global pred
global movies
p = pred
m = movies
tmp = pd.DataFrame(p.loc[user,:].T)
tmp['movieid']= tmp.index
tmp.columns=['predict','movieid']
tmp.sort_values('predict', ascending=False, inplace=True)
tmp=pd.DataFrame(tmp.head(10))
tmp=pd.merge(tmp, m, on='movieid')
return tmp
r= rec(196,10)
r

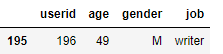
추천 결과. 196번 사용자는 49세의 남자이고 직업은 작가이다. 액션이나 공상과학 영화 같은 영화가 없다.(u.user 데이터 셋을 따로 다운 받아서 해석을 가미하였다.)
다른 사용자들에 대한 추천결과.


28살의 남자이며 관리직을 맡고 있는 사람이다.

41살 프로그래머 남자.
아이템 정보 데이터를 불러와서 조인을 한다.
u.user라는 또다른 데이터셋을 조인하여 살펴본 결과 196번 손님은 49세에 남성 직업은 작가이다. 어찌됐건 구현의 목적을 달성하였다.
추천시스템에서 정확도 바로 뒤로 따라오는 것이 계산량과 관련된 연구인데 이러한 SVD 모델 기반으로 계산량을 줄일 수 있어서 너무 좋았고, 또한 이미 나온 연구결과를 토대로 정확도 까지 좋다하니 정말 최신 기술이나 기법에 대해 공부를 많이 해야겠다는 생각이 든다.
7. MAE 구하기
기존에 전통적인 협업필터링에서는 sparse한 문제 때문에 모델 정확도를 구할 때, 실제 평가되어진 것들에 대해서만 계산이 가능했지만, 이렇게 $R_{reduced}$를 만듦으로써 모든 사용자에게 모든 아이템에 대한 예측 평점을 만들어 버릴 수 있다. SVD자체의 수학적 지식은 난이도가 쉽지만은 않지만, 구현은 더 쉬워졌다. MAE는 모델의 성능을 평가하기 위해서 사용한다는 것으로만 알고 굳이 구현은 하지 않는다.
논문에서는 고차원일 때와 저차원일 때의 각각 행렬에 대한 예측을 통해 MAE 를 구하여 비교하였다. 저차원일 때 MAE가 더 낮게 나와 성능이 더 개선되었다고 한다.
reference:
[1] Applying SVD on Item-based Filtering(2005)
[2] https://darkpgmr.tistory.com/106
[선형대수학 #4] 특이값 분해(Singular Value Decomposition, SVD)의 활용
활용도 측면에서 선형대수학의 꽃이라 할 수 있는 특이값 분해(Singular Value Decomposition, SVD)에 대한 내용입니다. 보통은 복소수 공간을 포함하여 정의하는 것이 일반적이지만 이 글에서는 실수(real) 공간..
darkpgmr.tistory.com
[3]https://grouplens.org/datasets/movielens/
'추천시스템' 카테고리의 다른 글
| 추천시스템에서의 유사도 지표와 피드백 특징 연구. (0) | 2020.10.23 |
|---|---|
| 메모리 기반 CF 추천시스템의 문제점 (0) | 2020.08.23 |
| surprise를 활용한 협업필터링(collaborative filtering) (3) | 2020.02.13 |
| 메모리 기반 하이브리드 필터링 구현 (0) | 2020.02.06 |
| MovieLens 데이터를 활용한 Collaborative Filtering 구현 (0) | 2020.01.15 |



댓글