이번 장에서는 차원을 축소하는 방법에 대해서 알아본다.
차원의 저주(curse of dimensionality)는 분석하는 데이터가 차원(feature)이 커지면 커질수록 row dimension에서 일어나지 않은, 기대하지 않은 현상들도 일컫게 되어 학습모델을 잘 만드는데 있어서 안좋은 요소로써 작용한다.
샘플을 늘리지 않는 상황에서 독립변수만 늘리게 되면 sample space가 굉장히 커지게 된다. 아래의 그림처럼 1차원에서는 5개의 샘플로 채웠던 것이 차원(feature, axis)이 증가할수록 sample space는 커지게 되어 데이터를 설명하기위해 필요한 데이터도 당연 늘어나게 되고, 이러한 차원이 계속해서 많아지게 되면 데이터의 패턴을 파악하기가 힘들어진다. 즉 모델을 만들기 까다로워진다. 예를 들어 선형회귀 같은 경우 변수하나 추가되면 학습해야할 parameter도 하나 늘어나게 된다. 게다가 변수간의 관계도 고려해야한다. 차원이 많다고해서 데이터를 더 잘설명해주진 않을까? 라는 것은 오판이다.

학습데이터의 차원이 증가할 때 성능이 좋아지다가 일정구간이 지나면서 성능이 감소하게 된다. 관측치를 늘려서 정보량을 늘릴수도 있다. 즉 sample의 수를 늘려서 우리는 더 많은 정보를 얻을 수 있는데, 차원을 늘리는 경우에는 마찬가지로 정보를 얻긴 하는데, 그만큼 모델복잡도도 증가한다는 것을 염두에 두어야 한다.
그래서 어떻게 하면 이렇게 차원이 많아 모델이 복잡해지는(데이터 패턴을 파악하기 힘든) 문제를 해결할 수 있을까?

차원이 증가하면 모델복잡도가 증가한다. 그래서 불필요한 변수를 제거하는 방법을 사용한다. 아래의 demensionality reduction 이 바로 그것이다.
차원을 줄이는 방법은 크게 두가지로 존재한다. selection과 extraction이다.
feature selection은 이미 존재하는 변수들 중에서 더 의미있어 보이는 변수를 골라내는 것이다.
반면에 extraction은 input 데이터 전체를 보고 새로운 변수를 생성하게 된다. 이 때 새로 생성된 변수의 개수는 기존의 변수를 압축했다고 생각하면 되기 때문에 곧 줄어든다고 할 수 있다. extraction 같은 경우는 선형/비선형 적인 방법으로 나뉜다. 생성된 변수들이 기존 변수들의 선형결합으로 표현가능하면 linear method라고 하고 그렇지 않으면 nonlinear method라고 한다.

이제 PCA 에 대해 알아본다.
PCA(Principal Component Analysis)는 feature extraction 방법이다. feature extraction 방법 중에서도 선형방법에 해당한다. 좀 더 수학적으로 말하면 일종의 orthogonal transformation matrix를 구하는 방법이다. orthogonal 이라는 것은 우리가 얻은 새로운 변수들이 서로 다 직교하게 만든 다는 것이다. 예를 들면 diagonal matrix에서 offdiagonal(대각원소 부분이 아닌)이 전부 0인 데이터이다. 선형대수적으로 생각해보면 모든 columns vector가 linear independent 하다는 것과 동일하다.
실제 데이터에서는 상관관계가 아예 없는 변수들로만 이뤄진 경우는 흔치 않다.
하지만 PCA같은 경우는 이렇게 실제 세계에서 어느정도 상관관계(correlationship)가 있는 데이터셋이 주어질 때, 이 데이터셋에서 변수들을 상관관계가 없는 변수들로 바꿔주는 역할을 한다.
PCA는 기존의 데이터가 갖고 있는 정보를 최대한 유지하면서 변수를 압축시켜준다고 할 수 있다. 하지만 정보라는 것은 다양하게 해석이 가능하다. unsupervised 해당하는 feature extraction방법 같은 경우는 유지하고자 하는 샘플 사이에 관계, 변수 사이의 관계를 산정한다. 그걸 기반으로해서 정보를 유지하면서 차원을 줄일 수 있게끔 하게 되는데 아래의 그림을 보면서 살펴보자.
PCA 는 순차적으로 변수들을 찾아 간다. 가장 중요한 변수는 분산(variance)이 굉장히 큰 axis를 말한다.
PCA같은 경우는 linear combination으로 새로운 axis를 찾는 것이다. 아래 그림의 관측치인 검은점들을 이 axis에 직교하게 사영(projection)을 시켜 새로운 univariate(일변량) 한 분포를 얻게 된다. 그리고 사영된 값들의 분산을 측정해서 그 분산이 가장 크게 되는 axis를 찾는다. 가장 큰 분산을 가진 것이 첫번째 principal component가 된다.
아래의 그림에서 관측치들이 어느정도 선형관계가 있는 것처럼 보이지만, 새로운 axis에 사영이 된 좌표로 표현하여 더는 선형의 관계가 없는 데이터로 만들어주는 것이다.

분산을 크게 해주는 axis를 찾는다는 것을 text의 classification문제로 생각해보면, 각 class별로 포함된 단어들이 그 class에만 포함된 그런 단어들이라면 더욱이 데이터를 class별로 잘 분리를 해줄 수 있는 데이터에 해당된다. 아래의 표를 보면 Floors 변수 같은 경우에는 층 정보로 어떤 label을 분리하기에는 정보가 부족해 보인다. 하지만 Value 변수를 보게 되면 그 분산이 Floors보다 커서 그런지 label을 분리하기에 좀 더 좋은 정보로 보인다. 이것이 위부터 설명했던 분산이 큰 axis를 찾는 것과 연결지어 생각하면 된다. 가장 분산이 커질 수 있는 새로운 axis를 찾는 것이다.

PCA에서 새로운 axis를 찾으면(아래의 그림에서는 $w$) 기존의 좌표들을 사영시키고, 사영한 새로운 값들의 분산을 측정한다고 하였다. 아래의 $x$벡터를 사영한 $t$ 벡터를 알고 싶으면 $w$ 의 방향벡터와 $x$ 벡터 사이의 내적 $t = w \cdot x$ 을 구하면 된다.

아래의 식에서 $w$ 의 좌표는 방향만 표현하기 위한 단위벡터이고 $x$ 좌표가 주어져 있다. 이들의 내적으로 실제 $t$의 값을 구할 수 있다.

PCA 하는 방법에 대해 알아보자.
위의 그림에 $w$와 같이 first component를 찾아야 한다.($w_{1}$)
먼저 모든 변수들에 대해서 평균을 0으로 만들어 준다. 이는 각 변수들마다 평균값을 구하고 값들에 해당 평균을 빼줌으로써 완성된다. 이 분산을 최대화한다는 것을 설명하기 위해서 분산에 대한 기댓값은 다음과 같다. $Var[X] = E[(X-E(X))^{2}] = E[E(X^2)-E(X)^{2}]$ . 여기서 평균이 0이라 하면 $E(X)^{2}$ 부분이 0이 되서 결국 $E[E(X^2)]$ 로 $Var[X]$를 구하게 되고 이를 이용한 식이 아래의 첫번째 식이다.
아래의 $w_{1}$ 같은 경우는 위의 그림에서 보았듯이 사영된 값들과 기존의 변수의 값들의 내적을 제곱한 것들의 합. 즉 분산이 가장 최대가 되게 하는 것을 말한다.

아래는 matrix 형태로 수식을 표현한 것이다.

$Xw$ 를 matrix로 표현하였고, 결국 $(x_{i} \cdot w)^{2}$ 에서 처럼 제곱을 하는 것은 $(Xw)^{T}(Xw) = w^{T}X^{T}Xw$ 로 표현되는 것을 알 수 있다. 아래의 식에서 $||w|| = 1$은 단위벡터를 가정하는 것이고, 전체적으로 값이 max 가 되게 하는 $w$를 찾는 목적으로 식을 구성하게 된다.

위의 수식은 아래의 식과 동일하다. $w^{T}w$는 $||w||$처럼 길이를 나타내고 단위길이라 했으니 1이니까 사라진 것이고, 이를 나타냈을 뿐이다.

길이에 제한을 두는 이유는 아래의 식처럼 변수와 $w$간의 곱의 제곱을 하는 과정에서 $w$가 방향은 같은데 길이가 달라서 값이 달라지는 문제에 대한 패널티를 주기 위해서 이다. 이 패널티를 주지 않게 되면 $w$의 길이가 길어서 분산이 더 커지는 문제가 발생하기 때문이다.

그래서 이 최적화문제를 풀기위한 방법은 $X^{T}X$에 대해서 eigenvalues를 구하고, 가장 큰 eigenvalues를 가지고 있는 $X^{T}X$ 행렬의 eigenvectors 가 바로 $w_{1}$이 된다. "공분산 행렬의 eigenvectors 를 구한다."
그리고 아까 위에서 언급했듯이 평균을 0으로 맞춰줬기 때문에 분산의 기댓값 $E[E(X^2)]$는 $X^{T}X$ 이며, 결국 covariance matrix와 비례하게 된다는 사실도 알 수 있다.
아래는 두 변수 간의 covariance를 구하는 식이다.


아래는 각 변수간의 cov를 구한 matrix이다.

아래의 비례한다는 것을 증명하기 위해 위의 $Cov(X,Y)$를 보면 우린 평균을 0으로 맞췄고 결국 모든 $C$ matrix의 cov들은 각 변수들의 내적으로 구성되게 된다 .

잠시 eigen vector와 value에 대해 간단히 살펴보고 가도록 하자.

어떤 $A$ matrix가 있을 때, 여기에 벡터 $x$를 곱한 것이 벡터 $x$와 스칼라 곱과 동일하게 되는 경우, $x$를 $A$의 eigen vector라 하고, 우항의 $\lambda$를 $x$의 eigen value라고 한다.
아래의 예를 보면 벡터 $x$, $y$ 가 각각 고유벡터인지 아닌지를 보여준다.

고차원 상에서 고윳값분해는 손으로 풀기 어려워 컴터를 활용하게 되고, PCA를 통해 이제 $X$를 처리하여 새로운 matrix를 생성한다고 할 수 있는데, 아래의 수식처럼 $k$ 번째 matrix를 구한다. n x p 행렬이 있으면 PCA를 하고서 n x p 의 행렬로 나올 수 있고, p-1, ... , 1 까지 extraction을 할 수 있다.
$k$번째 주성분을 찾기 위해서는 그 이전까지 찾았던 모든 주성분에 대한 사영된 정보들을 기존의 데이터 행렬에서 모두 빼준다. 그리고 남은 정보들 중에서 또 사영시켰을 때 분산이 최대가 되는 새로운 axis를 찾으면 되는 것이다.

그런 다음에 앞에 했던 방법과 동일하게 또 분산이 최대가 되는 axis를 찾으면 된다. 남아있는 eigenvector를 활용하는 것을 의미한다. 예를 들면 $w_{2}$의 경우에는 두번째로 큰 eigenvector를 사용한다.

정리하면, $X^{T}X$ 는 positive semi definite 하고 symmetric 하기 때문에 eigenvalue가 0보다 큰 값을 가지고, eigenvector들은 서로 직교하는 특징을 지니고 있다. eigenvector를 모두 구하고, eigenvalue들로 내림차순으로 정렬을 해서 큰 것부터 주성분의 순서를 구할 수 있게 된다.
$W$를 활용해서 $X$와의 곱으로 $T$를 구하는 것을 나타낸 식은 아래와 같다.

아래의 식은 주성분들을 column vector형태로 표현한 $W$ 이다.

$W_{l}$은 p x l 행렬을 의미한다.

여기서 $ p > l $ 로써 생각을 해보면, $p$ 개의 주성분을 모두 사용하지 않기에(갈수록 분산이 작아지는 $w$ 이기 때문에.) 여기서 Dimensionality reduction(차원축소)의 개념으로도 사용이 된다. 아래의 수식처럼 $l$ 개까지의 주성분행렬(truncated transformation)로 계산한다. 최종적으로 n x p 에서 n x l 로 축소된다.

아래의 그림은 PCA를 통해서 주성분을 시각화한 것이다. 원래 값은 2dim 축을 토대로 값들이 점들로 찍혀져 있는 것이고, 양의 상관관계를 보이는 것을 알 수 있다. 첫번째로 우상향하는 axis에 사영시킨 것이 가장 분산이 크게 되는 $w_{1}$ 벡터가 되고, 이에 직교하는 좌상향하는 axis가 $w_{2}$벡터가 된다. 기존의 차원 p 가 2 차원이여서 최대 2개까지의 axis를 구할 수 있다.

아래의 데이터를 가지고 실제로 PCA가 진행되는 과정을 살펴보도록 하자.

step1)
두 개의 변수 x, y 가 있다. 우선 평균이 0이 되게 하기 위해서 각 컬럼의 평균을 구하고 평균값을 빼준다. 평균값을 뺀 결과가 아래의 표와 같다.

step2)
위에서 평균을 0으로 맞춰줬기에 co-variance를 구하는 식에 대입만 하면 된다. 아래의 파이썬 코드로 계산하여 그 결과가 같음을 확인해보았다.



step3)
이제 구한 cov matrix의 고윳값과 고유벡터를 찾는다. 계산은 생략하였다. eigen value는 1.28, 0.049 로 나온다. 이에 상응하는 주성분벡터인 eigen vector들은 아래와 같다.
주성분벡터는 반드시 unit vector로 맞춰주어야 함을 염두에 두어야 한다. 아까 설명한 것 처럼 그 길이에 따라 분산이 달라지는 것을 막기 위함이다.


step4)
아래의 W 와 같이 $w_{1}, w_{2}$ 를 columns vector로 넣은 matrix를 얻을 수 있다.

만약에 dimension을 줄이고 싶다면 first principal component를 구하면 된다.

그리하여 새로운 데이터 셋을 얻을 수 있게 된다.

주성분을 모두 활용하면 아래와 같이 기존의 2차원 그대로 새로운 데이터셋을 얻게 된다.

만약 첫번째 주성분만 사용해서 새로 데이터셋을 얻고 싶으면 위에서 언급했든 first principan component를 사용하면 된다. 첫번째 주성분만 사용하여 얻은 새로운 데이터 셋은 1차원의 feature로 구성된 데이터셋이 된다. $W$(1x2) $\cdot$ $X$(2x10) = (1x10) 행렬이 나오는 것 처럼 말이다.
PCA를 통해 만들어진 새로운 axis들은 보통 전처리 단계로써 사용이 된다. 100차원을 2차원으로 PCA한 결과, 2차원의 axis를 시각화를 해서 보면 샘플사이의 관계를 보는 용도로 쓴다. 또는 데이터 차원을 줄여서 모델을 만드는 용도로 사용된다.
장점은 $W$와 같은 loading matrix를 통해서 낮은 차원으로 바로 보낼 수 있다. 데이터 특성만 파악하는 정도로 사용할 때도 있다. 단점은 새로운 데이터가 오면 다시 extraction을 진행해야하는 부분이 있어서 모델만드는데는 적합하지 않은 경우도 있다.
변수들의 scale에 영향을 받는 것에 대해 알아보자. 아래의 경우는 scale이 10배차이가 나고 분산은 제곱인 10000배 차이가 난다. PCA를 적용하기 전에, variance도 unit variance로 맞춰 준다. 분석과정에서 분산도 미리 맞출 수도 있다.

liear transformation의 장점으로 다시 복원할 수 있다라는 것이 있다. 아래의 식처럼 새로운 데이터 셋을 얻었다고 해보자.

$W$의 unit vector가 서로 직교한다면 $W$는 $W$의 역행렬인 $W^{T}$와 같아져 아래와 같이 나타낼 수 있다.


그리고 zero mean을 만드는 과정을 거쳤다면 다시 mean을 더해주면 된다.

p차원을 $l$ 까지의 주성분행렬을 만들었다면 정보소실이 되긴 하지만 $W$의 전치행렬을 곱함으로써 원래 차원으로 변환을 시켜줄 수는 있다.
또다른 feature extraction인 Multidimensional Scaling(MDS) 에 대해 알아보자.
맵핑이 가능한 것과 아닌 것이 존재하는데, 맵핑이 불가능한 것은 non linear 한 것이 대부분이다. MDS는 PCA처럼 axis를 찾는다니 보다는 원하는 차원의 데이터로 바꿨을 때 좌표 값이 어떻게 바뀌는지 계산하는 방식으로 feature를 extracion 한다. MDS 는 고차원의 데이터 같은 것을 2차원과 같은 저차원으로 축소하여 시각화함에 많이 사용을 한다.
보존해야 하는 정보를 좌표 사이의 거리로 산정한다. i, j는 각각 i번째, j번째 샘플이다. i 와 j 사이의 거리를 d(i,j)라 하면 이들의 Dissimilarity matrix를 구한다.

MDS는 원래 데이터셋에서의 두 좌표사이의 거리와 최대한 유사하도록 transformed vector $y$ 를 찾는 것이 목적이다.

만약에 고차원에서 distance measure를 유클리디안을 사용한다라고 하면, $d(i,j) = ||x_{i} - x+{j}||$ 로 사용하게 되고, 목적은 저차원 벡터인 $y$를 찾아서 $||y_{i} - y_{j}|| \approx ||x_{i} - x_{j}||$ 로 표현할 수 있게 하는 것이다.
그래서 최적화해야 하는 이 목적함수를 아래처럼 표현이 가능하다. 애초에 처음부터 좌표를 알아야지만 적용할 수 있는게 아니다. 위의 $D$ 처럼 dissimilarity matrix만 있으면 적용이 가능하다.

그래서 좌표는 없지만 거리를 표현하는 데이터가 있으면 사용이 가능하다. 아래의 그래프는 단어 사이의 거리를 알고 표현한 것이다. 이럴 때 MDS 를 적용하면 2차원에 아래와 같이 표현이 가능하다는 것이다.

다음으로 Feature Selection에 대해 알아보자.
Feature Selection 는 새로운 변수를 뽑아내는게 아니라 최적의 feature를 고르는 것이다. 예를 들어 유사한 변수가 있으면은 그중에 하나만 쓴다던가 등이 있다. 일반적으로 대부분의 selection은 unsupervised 방식으로 하기보다는 target variable을 더 잘 맞출 수 있는 방법(supervised)으로 사용이 된다. 여기서는 Filter에 대해서만 설명한다.

Filter 방식은 target 과 feature사이에 점수를 측정하고, 점수를 기준으로 순위를 매겨서 상위 k 개를 선정하는 방식이다. 굉장히 빠르게 subset을 구성가능하고, 다양한 방식이 있다.
단점은 input , target 간의 관계를 고려하기 때문에 input 끼리의 관계를 고려하지 않는다.
Wrapper 는 모델을 학습해서 그 모델의 성능을 기준으로 찾는 것이다. cross-validation을 해서 여러 모델을 구성하고 가장 성능이 좋은 모델의 feature를 선택한다. 이러한 방식 같은 것은 애초에 feature가 많아서 줄이고자하는 경우에는 정말 많은 조합에 대해서 작업을 모든 것에 대해 해줘야 한다.
Embedded 애초에 모델 학습과정에서 feature선택을 할 수 있도록 하거나, 애초에 feature가 selection되는 모델이 만들어 지는 것들을 말한다.
Filter 방식
target과 feature의 타입에 따라서 점수를 측정하는 방법이 다 다르다.
1.1 둘 다 범주형 변수인 경우. crosstable을 구한 다음에 이것을 이용해서 target과 feature사이의 점수를 구하게 된다.
아래의 예는 target이 1,2, ... ,K 까지 있고, feature의 경우는 L 개이다. 각각 해당되는 셀에 개수를 카운팅함으로써 각 조합에 해당하는 값들을 통해서 점수를 계산한다.
대표적인 것이 Chi-squure 이 있다. 두 변수가 독립인지를 알 때 쓰던 카이제곱 검정통계량이다. $E$는 expectation을 의미한다. expectation은 아래의 식과 같다.

O와 E가 차이가 없을 수록 카이제곱 값은 작아지게 된다. 그리고 카이제곱 분포에서 검정을 통해 귀무가설을 기각하면 두 feature가 독립이다 라는 대립가설을 채택하게 된다.

기댓값을 구하는 것은 비중을 구하는 것과 동일하다.

그래서 최종적으로 카이제곱 값이 큰, 즉 target을 예측하는데 더 좋은 변수다라고 판단되는 feature를 골라서 사용하게 된다.
계속해서 Filter방법 중에 하나인 Pointwise mutual information 방법이 있다. 특정 변수, mutual information은 두 변수사이의 관계를 계산하는 건데, 아래는 각 변수별 조합으로 만들어진 결과가 나오게 된다. 아래의 수식에서 분모가 의미하는 것은 두 변수가 독립일 때를 나타내고 분자는 결합확률을 나타낸다. 즉, 독립일 때 대비 조합의 확률이 얼마나 큰 지를 계산해서 log를 씌운 것이다.

Mutual information(information gain)은 pointwise mutual information의 기댓값이라고 생각하면 된다. feature selection에서는 y가 target variable로 고정되어 있어서 $MI(x)$ 로 표기하였다. 원래는 두 변수의 관계를 계산하는 것이다.

샘플을 보고 확률을 쉽게 구할 수 있다. 전체 샘플 대비 몇 개 인지 이렇게 말이다.

다음에는 target은 categorical인데 feature는 numerical일 때이다. 이런 경우에는 feature 를 categorical로 바꾼다. binning한다라고 한다. 히스토그램을 그려 할당하는 방식으로 말이다.
아니면 F 검정을 사용한다. One-way ANOVA(Analysis of Variance)는 그룹 내에 관심있는 객체들이 있고, 또 그룹 별로 차이가 있는지 없는지를 검정하는 것이다. 선형회귀에서 ANOVA 테이블과 유사하다. 차이점은 SSE를 계산할 때가 좀 다르다. Between 그룹 간의 편차가 어떻게 되느냐이고, Within은 그룹 내의 편차가 어떻게 되느냐 이다.

이번에는 feature와 target 변수들이 모두 numeric인 경우를 보자. 이런 경우에는 선형적인 관계를 보고 싶다면, 피어슨 상관계수를 구한다.

상관계수에 대한 검정은 t 검정을 진행한다. t값에 제곱을 취해 F 통계량으로 카이제곱분포로 검정을 하게 된다. 자유도는 n-2.

mutual information을 적용할 수 있다. numerical 변수에 대한 적분으로 구한다.
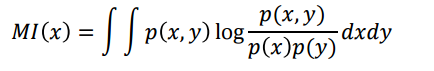
target이 numerical이고 feature가 categorical이면, 마찬가지로 F 통계량으로 selection이 가능하다.
'머신러닝' 카테고리의 다른 글
| Ensemble Methods (0) | 2020.11.29 |
|---|---|
| Expectation Maximization (1) | 2020.11.24 |
| Support Vector Machine(2) (0) | 2020.11.06 |
| Nearest Neighbor Method (0) | 2020.10.18 |
| Support Vector Machine(1) (0) | 2020.10.18 |




댓글