이번장에서는 앙상블 기법에 대해 알아본다.

앙상블로 학습한다는 것은 일종의 meta learning algorithm이다. 즉 데이터가 주어지면 바로 모델링을 하는 것이 아니라, 여러 모델들을 결합해서 보다 나은 성능을 얻는 최종적인 모델을 만들기 위한 방법론에 해당한다.
여러개의 모델을 합쳐서 최종적으로 예측을 하기 때문에 중점적으로 고려해야하는 것은 어떻게 서로 다른 모델들을 주어진 데이터를 이용해서 만들어낼 것인가와 각 모델의 결괏값을 병합할 것이냐가 있다.
앙상블 모델을 설계하기 위한 방법에는 여러 방법이 존재한다.
1) bayesian voting
parametric한 방법으로 데이터를 분석한다면 데이터에 대한 분포를 가정한다. 예를 들어 선형회귀 같은 경우는 설명변수와 종속변수사이의 관계가 선형관계이고, 오차항은 정규분포를 따른다는 예시들이 있다. 실제로 하나의 모델을 선택한다는 것은 이러한 가정을 따른다 결정하는 건데, bayesian votion은 데이터 분포에 대한 가설들을 각 모델별로 가정하고 생성하자는 것이다. 아래의 수식은 전확률을 나타내고 있다.
bayesian probabilistic 으로 세팅할 때는 각 가설 $h$ 를 조건부 확률 분포로 정의 한다.

새로운 데이터 샘플 $x$ 가 주어지고 학습 샘플 $S$가 주어질 때, 예측값 $f(x)$ 는 $P(f(x) = y|S,x)$ 를 계산하는 문제로 볼 수 있다. 이는 모든 가설 ℋ 에 대한 weighted sum 이라 할 수 있다.

2) Manipulating the training examples
두번째는 새로운 샘플을 생성하거나 중복 추출하는 등의 방법을 말한다. 여기서는 input feature를 그대로 두고 실제 origin 데이터 셋과 비슷한 새로운 데이터셋들을 생성한다. 샘플들을 달리해서 모델링 결과를 다르게 나오게 한다. 이 방법같은 경우는 unstable learning algorithm 에서 좋은 성능을 낸다. unstable algorithm은 약간의 변화가 발생하면 모델의 성능이 많이 달라지게 되는 알고리즘을 말한다. 특히 아래의 그림처럼 knn 에서 k가 작을때의 예가 있다. Decision tree, neural network, knn들은 k 가 작은 경우 unstable하다고 알려져 있으며, 상대적으로 support vector machine이나 linear regression의 경우는 stable 하다고 알려져 있다.
아래의 경우는 knn 에서 k가 각각 1일 때, 10일 때를 나타낸다. 왼쪽그림 같은 경우는 근접이웃 1명의 정보만을 가지고 예측을 하기에 bias는 낮지만 분산이 엄청커지니까 overfitting 된다는 것을 확인할 수 있다. 또 boundary 관점에서 보면, k 가 1인 경우에는 샘플이 약간만 변해도 boundary가 많이 변할 것이고, k가 10인 경우를 보면 클러스터 내의 샘플이 조금 변해도 boundary가 크게 변하지 않는다는 것을 알 수 있다.

3) Manipulating the input features
2)와 비교하면, raw는 그대로 주는 상황에서 columns의 subset을 생성해 새로운 데이터셋을 구성해서 개별 모델들을 만드는 방법이다.
4) Manipulating the output targets
input은 그대로 두고, target을 변형해서 새로운 데이터셋을 만든다. 앞전에 'support vector machine(2)'장에서 $\nu$-SVC 의 one-versus-the rest방식 one-versus-one 방식처럼 binary boundary를 여러개 만들어서 최종 예측을 하는 것과 이를 변형해서 multiclass를 예측하는 방식을 보았는데, 그러한 방식이 여기에 해당된다고 할 수 있다.
5) Injecting randomness
초기에 initial의 값에 따라 결과값이 많이 달라지는 경우를 생각해보자. neural network 알고리즘의 경우 초기에 구조를 셋팅하고, 초기 weight 값을 어떻게 셋팅하냐도 성능에 영향을 준다. 즉, 서로 다른 weight를 만들고 그것들에 대한 최종결과를 합쳐서 사용하게 된다.
여러 모델을 합치고, 결과를 결합했을 때 하나의 모델을 사용하는 것 보다 앙상블기법이 좋은 이유에 대해 알아보자.
데이터에 맞지 않는 모델을 사용할 수도 있고, 또한 하이퍼 파라미터의 초깃값 설정 등으로 인해 발생하는 risk들을 줄일 수 있다고 보면 된다.
-1. statistical reason: A learning algorithm 은 가설 공간 $H$가 있을 때, 그 가설공간에서 좋은 가설을 선택하여 별로 좋지 않은 가설로 학습한 모델의 낮은 성능에 대한 risk를 줄일 수 있게 된다. 즉 true 값을 예측하기 위해서 좋은 가설을 찾는 것이다.

-2. Computational reason: 마찬가지로 계산적인 문제에서의 이유도 존재한다. 최적화 관계에서 global minimum 에 도달못하는 모델을 사용했을 때, 안좋은 local minimum에 빠지는 확률을 줄어들게 할 수 있다. 앙상블로 서로다른 셋팅에서 평균내서 사용해서 risk를 줄이자!

-3. representational reason: representation 측면에서 보면, 서로 다른 학습 알고리즘의 경우는 수식이나 가정을 각각 다르게 사용하기 때문에 표현할 수 있는 함수들의 공간이 제한되어 있다. 그래서 하나의 함수만을 사용하면 실제 데이터를 학습할 형태의 제약이 생기게 된다. 잘못된 모델을 선택하게 되면 실제값을 표현할 수 있는 공간 밖에 있을 수도 있다. 즉 앙상블하면 표현할 수 있는 함수의 형태도 많아지니 성능도 더 좋아지게 된다.
그런데 이 이슈의 경우는 딥러닝 같은 경우는 표현 공간이 매우 넓어서 이 부분은 큰 이슈로는 여겨지지 않는 수준이다. ₩

본격적으로 앙상블 기법의 알고리즘에 대해 알아보자.
앙상블 기법을 볼 때 크게 두가지로 나눌 수 있다. 크게 Bootstrap aggregating(Bagging) 과 Boosting이 존재한다.
1. Bootstrap aggregating(Bagging)
배깅이라는 것은 기본적으로 앞에서 모델을 만드는 과정 중에서 "2) Manipulating the training examples" 을 떠올려보면 된다. 학습 데이터셋에서 서로 다른 subset을 만들게 되고 서로 다른 모델들을 만들게 된다. 이 때 배깅이 사용하는 방법이 bootstrap sampling이라고 한다. 부트스트랩 샘플링이라고 하면은 다음의 두가지를 만족하면서 샘플링을 하겠다는 것이다. 첫번째, uniformly 하게 샘플링하기이다. 모든 샘플에 대해서 샘플링될 확률이 uniform 하다는 것이다. 동일하다는 것이다. 두번째, 샘플을 복원추출하는 것이다. 뽑힌 것도 또 뽑힐 수 있게 샘플링하겠다는 것이다.
아래의 그림은 배깅 프로세스를 나타내는 그림이다.
원래 데이터 셋 D에서 원하는 만큼의 부트스트랩 샘플 데이터셋을 만들고 개별 모델을 생성한다. 이 후 개별 모델의 결과를 종합하게 된다.

아래의 그래프는 배깅을 했을 때가 개별모델을 사용했을 때보다 얼마나 안정적인 지를 보여주는 그림이다. 회색의 선은 100개의 서로 다른 부트스트랩 표본으로부터 얻어진 smoothing 결과이고 빨간선은 100개의 결과를 종합한 선이다. 확실히 평균을 나타낸 빨간선이 더 stable 하고 noise한 지점에 대해 overfit이 덜 한 경우를 알 수 있다. 일반적으로 부트스트랩을 이용해서 모델을 합쳐 사용하게 되면 최종 모델의 bias는 크게 증가시키지 않으면서 noise에 크게 영향을 받지 않게끔 할 수 있다.

배깅에서 변형된 형태인 Weighted Aggregation(Wagging) 이라는 것이 있다. weight를 샘플링할 때 다르게 주는 차이를 가지는 방식이다.
2. Boosting
부스팅 알고리즘에 대해 알아보자.
부스팅 알고리즘은 반복적으로 모델을 학습하게 된다. 예를 들어 모델을 학습하고, 또 학습하고, 또 학습하고 .. 순차적으로 n 의 모델들을 학습하게 된다.
weak learner : 실제 output 하고의 연관성이 강하지는 않은 것을 의미한다.
strong learner : output 과의 연관성이 굉장히 강한 것을 의미한다.
개별적으로는 성능이 안좋아도 합쳐놓으면 strong learner가 되더라는 것이 부스팅 알고리즘의 핵심 아이디어이다.
weak learner 가 어떻게 strong learner 로 바뀌냐 하면, wear learner 를 통해 예측을 하고, 그 weak learner의 정확도에 따라서 weight를 생성하여 다시 학습셋을 구성하게 된다. Bagging, Wagging과의 차이는 부스팅 알고리즘은 순차적으로 학습 모델을 오차에 대한 weight를 가지고서 strong하게 업그레이드 시켜나가는 것이다.
일반적으로는 분류문제의 경우는 오분류인 경우에 weight를 이전 보다 더 증가시키고, 오분류가 전보다 나아지면 weight를 더 낮춰주고, 그러므로 틀린 애들을 더 참여시켜 좀 더 학습에 사용하도록 하는 것이다.
아래의 그림을 보자. 배깅 같은 경우에는 원래의 데이터 셋에서 여러개의 서브셋을 만들고 개별모델을 만드는 것을 볼 수 있다. 즉 병력적으로 만든다고 볼 수 있다. 부스팅 경우에는 서브셋을 업그레이드 시켜나가는 것이 보이며, 순차적으로 진행하니 병렬처리가 불가능하다.

부스팅 알고리즘에서도 다양한 알고리즘이 존재한다. 이번 장에서는 Adaptive Boosting 에 대해 알아본다.
- Adaptive Boosting(AdaBoost)
앞선 부스팅 알고리즘의 방식을 그대로 기용하고 있다. 순차적으로 weak learner 를 학습하고 weighted manner 로 합쳐서 최종 예측을 하게 된다. 최종 모델을 수식으로 표현하면 아래와 같다. T 가 의미하는 것은 T 개의 weak learner를 합쳤다고 생각하면 된다. 그리고 소문자 t 는 각 step 을 나타낸다. 각 스텝에서 input $x$를 가지고 만든 개별모델 $f_{t}(x)$ 를 모두 결합하여 최종적인 모델 $F_{T}(x)$를 얻게 된다. $f_{t}(x)$는 안에 weight 까지 포함되어 있다는 것을 상기하자.

부스팅 알고리즘에서 학습을 할 때 순차적으로 해야만 하는 이유가 이전 단계 까지의 학습된 weak learner 들의 성능을 고려를 해서 데이터들의 weight 를 조절하기 때문이라고 하였다. 그래서 결국은 t 라는 시점에서 t-1 시점인 이전까지 합쳤던 모델과 새로 더하게 되는 t 시점에서의 모델을 더해서 예측을 했을 때 그것을 minimize 하게끔 하면서 가중치도 구한다. 아래의 수식은 그래서 오차와 같이 생각하면 된다.

앞에서는 그냥 일반적인 Adaptive Boosting에 대해서 설명한 것이다.
그렇다면, 각 단계별로 어떻게 학습하고 weight를 조절하고 알파값을 조절하는지 알아보자. 가장 심플한 케이스인 이진분류 문제에 대해서 설명해본다. 다음과 같은 데이터 $D$ 를 가지고 있다고 해보자. $ D = \left\{ (x_{1}, y_{1}), ..., (x_{n}, y_{n}) \right\}, y_{i} \in \left \{ 1, -1 \right\}$ $x$는 input vector 고, $y$ 는 target vector 이당. 이 때 weak learner 셋 $\left \{ h_{1}, ..., h_{T} \right \}$ 에 대해서 각 모델에서 예측값이라 할 수 있는 것은 $h_{j}(x_{i}) \in \left \{ 1, -1 \right \}$ 라고 할 수 있다.
아래의 수식을 보자. $F_{t-1}(x_{i})$ 는 이전까지의 weak learner들을 합쳐놓은 것이라 정의를 한다.

위의 수식에다가 현재 시점의 weak learner 를 더하게 되면 최종적으로 아래의 수식처럼 $t$시점의 모델이 된다.

목적은 $\alpha_{t}, h_{t}(x_{i})$ 를 구하는 것이다. 앞서 E function을 정의하였다. 오차가 최소가 되게 하는 weak learner를 만들겠다고 했는데, 그러면 어떻게 최종적으로 E를 결정할까?
Adaptive Boosting 같은 경우는 exponential loss를 사용하는데, 전체 error는 각 데이터 샘플의 exponential loss 의 합이 되겠다.
아래의 수식에서 $y_{i}$는 실제값을 의미하며, $F_{t}(x_{i})$는 $t$라는 시점에서의 예측값을 의미한다.

초깃값으로 weight 는 동일하게 1로 준다. 그리고 $t$ 시점에서의 weight 는 아래와 같이 정의를 한다. $w_{i}^{(t)}$는 각 샘플 $i$에 가해지는 weight을 의미한다.

그래서 아래의 수식과 같이 전개를 하게 되어 총 error를 구하는 식을 다시 표현할 수 있다.

$h_t(x_{i})$ 예측치가 정분류를 할수도 오분류를 할 수도 있고, 정분류인 경우, 오분류인 경우 두가지 summation 로 나뉘게 되고 아래의 수식 첫번째 줄처럼 두개의 term으로 나누어지는 것을 알 수 있다. 이진분류의 경우 1과 -1로 예측을 하게 되고, 정분류의 경우 부호가 같아서 같은 부호끼리의 곱이므로 양수로 나와 왼쪽 term에서 $-\alpha_{t}$ 인 것을 볼 수 있고, 오른쪽 term은 부호가 다른 수를 곱하기에 음수로 나와서 알파의 부호가 바뀐 것을 볼 수 있다. 즉, 정답을 맞추면 $y_{i}h_{t}(x_{i}) = 1$ 이 되고, 못 맞추면 $y_{i}h_{t}(x_{i}) = -1$ 이 되게 되어 아래 첫번째 수식처럼 나누어 표현할 수 있는 것이다.
그리고 나서 두번째 수식줄을 보자. 빨간색 동그라미를 친부분이 오분류에 대한 summation term인 것은 풀어서 전개하면 알 수 있다 즉, 모든 샘플 $n$ 개에 대해서 맞추지 못한 샘플에 대해서 맞춘 샘플에 대한 것 보다 큰 값을 가지게 된다. 그리고 오차를 줄이기 위해서는 맞추지 못한 것들에 대한 term인 빨간 동그라미 내의 수식을 minimize 해야한다.

수식을 보면 샘플 $i$를 포함하여 가지고 있는 것은 $w_{i}^{(t)}$ term 인 것을 알 수 있고, 아래의 term 을 minimize 해야한다. 실젯값을 맞추지 못했을 때의 $w_{i}^{(t)}$를 말이다. 즉 $w_{i}^{(t)}$ 가 큰 것은 더 틀리지 않게 하는 방향으로 나아간다. 앞전에 보았듯 $w_{(i)}^{t}$는 t-1 의 weight를 의미한다. 즉 t-1 까지 죽죽 weak learner 들을 업데이트 해나가면서 자꾸 틀려서 $w_{i}^{(t)}$ 가 높은 샘플을 더 틀리지 않는 방향으로 나아가기 위해 아래의 term을 최소화하겠다는 말이다. 즉 $h_{t}$ 는 아래의 수식을 최소화하는 $E_{t}$를 minimize 하게 된다. 그러므로 weak learner 는 lowest weighted error를 갖게 된다. 샘플에 $w_{i}^{(t)}$ 를 할당하고 예측을 하면 $h_{t}(x_{i})$ 가 된다.

$h_{t}$ 를 학습하고 나면 이제 $h_{t}$ 에 해당하는 $\alpha_{t}$ 를 구해야한다. 우리가 $h_{t}$ 를 구했으므로 모르는 것은 $\alpha_{t}$ 에 대한 것 밖에 없으므로, $\alpha_{t}$에 대해서 미분해서 0이 되게 하는 식을 푸는 과정을 진행한다.
$E_{t} = \sum_{y_{i}=h_{t}(x_{i})} w_{i}^{(t)} e^{-\alpha_{t}} + \sum_{y_{i} \neq h_{t}(x_{i})} w_{i}^{(t)} e^{\alpha_{t}}$ 를 $\alpha$에 대해 미분해서 0 이 되게 하는 과정을 진행해보자.
(1) $-\sum_{y_{i}=h_{t}(x_{i})} w_{i}^{(t)} e^{-\alpha_{t}} + \sum_{y_{i}\neq h_{t}(x_{i})} w_{i}^{(t)} e^{ \alpha_{t}} = 0$ exponential 에 - 만 앞으로 나오면서 전개가 된다.
(2) $e^{ \alpha_{t}} \sum_{y_{i}\neq h_{t}(x_{i})} w_{i}^{(t)} = e^{-\alpha_{t}} \sum_{y_{i}=h_{t}(x_{i})} w_{i}^{(t)}$ 반대쪽으로 넘겨서 전개를 하였고, 이제 exponential을 지우기 위해 log를 취한다.
(3) $\alpha_{t} + log(\sum_{y_{i}\neq h_{t}(x_{i})} w_{i}^{(t)}) = -\alpha_{t} + log(\sum_{y_{i} = h_{t}(x_{i})} w_{i}^{(t)})$ 처럼 로그를 취한 것을 계속 전개해 주어 알파에 관해서 계속 정리를 해주자.
(4) $2\alpha_{t} = log(\frac{\sum_{y_{i} = h_{t}(x_{i})} w_{i}^{(t)}}{\sum_{y_{i}\neq h_{t}(x_{i})} w_{i}^{(t)}})$ 에서 2를 나눠주면 아래의 수식으로 정리가 끝난다.

그런 다음에 아래의 입실론을 전체 weight 들에 대해서 예측 실패한 것들의 weight들의 비중으로 정의한다.
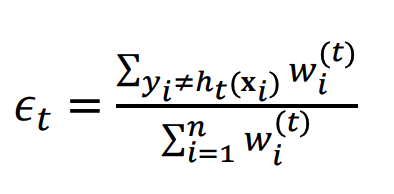
그렇게 되면 위의 수식을 아래처럼 단순한 형태로 바꿀 수 있다.

그래서 이제 무얼 하느냐? t+1 번째 샘플들이 가질 $w_{i}^{(t+1)}$ 벡터를 만들어주면 된다. 위의 식 $w_{i}^{t} \cdot e^{-y_{i} \alpha_{t} h_{t}(x_{i})}$ 를 계산하여 나온 벡터 값이 그대로 샘플들 하나하나에 $w$를 의미하게 된다. $y$는 벡터, $\alpha$는 스칼라, $h_{t}(x_{i})$ 는 벡터 형태로 되어 있고, 예를 들어 샘플 1번은 $y$의 첫번째 값 x $\alpha$ x $h_{t}(x_{1})$ x $(-1)$ 의 곱이 $e$에 지수로 올라가게 된다. 이런식으로 샘플 하나하나의 $w$를 update 해나가면서 다음 번째 알고리즘에서 샘플들의 weight를 쥐어주게 된다.
- Aggregation of Predictions
여러 모델로 생성된 예측 값들을 집계하여 하나의 예측값으로 만들어 주는 최종 단계이다.

분류 문제와 회귀 문제에 따라서 또 집계하는 방법이 나뉘게 된다. 먼저 분류문제에 대해 알아보자.
majority voting
kNN에서도 설명한 것과 동일하다. 가장 다수를 차지하는 클래스를 예측값으로 고르겠다는 뜻이다. 이런 방식을 hard voting이라고 부르기도 한다. 아래의 그림을 보면 세개는 클래스 1을 한개는 클래스 2를 할당하게 하는데, 3개의 모델에서 나온 것이 더 많으니 다수결로 최종적으로 클래스 1로 예측하겠다는 간단한 원리이다.

위의 경우에는 개별 모델별로 performance가 좀 다를 수 있고 또한 예측값도 조금씩 다를 수 있는데 그럴떄 좀 고려를 할 수 있는 방법이 soft voting 이다. 모델들의 weight 를 서로 다르게 주어 합치는 방식이다.
만약 사용하는 분류기가 확률모델이라고 한다면은 확률에 대해서 weight를 부여하게 된다. 아래의 그림을 보면 각 모델의 posterior(사후확률) p를 토대로 이 p를 합쳐서 예측값으로 사용한다. 그리고 아래의 p 가 확률로써 기능을 하기 위해서는 w 는 다 더하면 1이 되야한다.

만약 클래스에 대한 확률값으로 output 이 나오는 것이 아니라 output이 딱 클래스 하나를 뱉는 그런 모델인 경우에는 아래의 방법을 사용한다. 먼저 $I$는 indicator function으로 사용되며 input 값이 참이면 1 아니면 0을 뱉는 성질을 가지고 있다. $i$번째에 추정된 모델의 예측값이 참이면 1 아니면 0을 나타낸다. 그래서 예측값은 각 클래스별로 예측하는 것들에 대해 weight를 각각 더해서 weight 가 가장 큰 클래스 k 로 예측을 하겠다는 것이다.

그 다음은 회귀문제에 대해서 예측값을 집계하는 것을 알아보자.
가장 기본적으로는 평균을 내어서 사용하는 것이다. 샘플 $i$에 각 모델의 예측값이 각각 나오면 그것들의 평균값을 최종적인 $i$의 예측값으로 사용하는 것이다.

그리고 가중평균을 내어서 사용하는 것이다. 위의 경우는 weight가 모두 1이라고 할 수 있다.
중요도가 높은 모델에 weight를 더 줌으로써 예측 결과에 더 많이 반영하게 하는 것이다.

weight를 어떻게 결정할까에 대해서 알아보자.
- performance weighting
모델의 성능에 따라서 weight 를 할당하겠다는 것을 의미한다. $E$라는 것은 0~1 사이의 값을 갖는 성능 지표(MAE, precision 등)를 의미한다. 1에 가까울수록 모델의 성능 안좋은 것으로 기준을 잡고 $E$를 사용한다.

- Entropy weighting
분류문제에서만 사용할 수 있는 방법이다. 각 클래스에 대한 확률 값을 준다고 할 때, 그 확률 값들에 엔트로피를 계산하고, 이것의 역수에 비례하게끔 설정한다. 의사결정나무에서 엔트로피를 계산하는 것을 배웟는데, 모든 클래스에 대한 확률이 동일하면 엔트로피가 가장 크다. 한 클래스에만 모두 편중이 되면 엔트로피가 가장 작다. 그 말인 즉슨 특정 모델이 특정 클래스일 것이라 강하게 확신할수록 엔트로피는 작아지고, 확실성이 없어서 클래스 별로 확률값의 차이가 없으면 엔트로피는 커지게 된다. 하나의 클래스로 확실하게 예측할수록 더 큰 weight 를 준다고 할 수 있다.
performance weighting는 전체적인 모델의 성능에 대해 고정이 되어 있다고 한다면 entropy weighting 같은 경우는 개별 샘플별로 weight 가 다르게 산정이 된다. 그래서 특정 샘플에서는 확실성이 낮고 다른 것에서는 높을 수가 있으므로 새로운 input 이 들어오면 weight를 계속 다시 계산해주어서 output을 계산해낸다.

이론적으로만 보면 AdaBoost 가 다소 추상적으로 느껴져 직관적인 이해를 돕기 위한 사이트를 아래에 공유한다. 아래의 사이트의 process를 따라 가다보면 자연스레 어떻게 alpha, epcilon 을 계산하고, weight 가 어떻게 update 되고, 마지막으로 예측 값이 $\sum w \dot h(x)$ 로 계산되는 것을 이해할 수 있을 것이다.
sefiks.com/2018/11/02/a-step-by-step-adaboost-example/
'머신러닝' 카테고리의 다른 글
| Stochastic Gradient Descent 를 쉽게 이해해보자. (0) | 2020.12.16 |
|---|---|
| gradient descent(경사하강법) 를 쉽게 이해해보자. (0) | 2020.12.14 |
| Expectation Maximization (1) | 2020.11.24 |
| Dimensionality Reduction (0) | 2020.11.16 |
| Support Vector Machine(2) (0) | 2020.11.06 |




댓글