Abstract
GCN의 경우 협업필터링에 있어서 새로운 state-of-arts 로 등극했지만! 추천하는데 있어서 효율성에 있어서는 이해가 잘 되지 않는 경우가 많다고 할 수 있음!
GCN의 특징인 feature transformation and nonlinear activation 는 협업필터링 성능 향상에 기여를 별로 못하기도 하고, 추천성능도 그닥 안좋고, 학습하기도 까다로운 츼명적인 단점이 있음. 이 연구에선 GCN 디자인을 심플하게 하고, 추천에 있어서 정확하고 간결한 모델을 만드는데 그 목적이 있음!
특히 LightGCN은 사용자와 아이템 상호작용 그래프로 선형적으로 순전파하면서 사용자와 아이템 임베딩을 학습한다. 마지막 임베딩으로 모든 레이어에 대해 학습된 임베딩의 가중합을 사용한다.
1. INTRODUCTION
사용자 임베딩, 아이템 임베딩을 잘하는 것에 초점! Matrix Factorization과 같은 방법이 있죠. 그리고 나아가서 CF의 state-of-arts를 달성한 NGCF는 high-hop neighbors를 활용한 서브그래프를 사용합니다. 네트워크를 활용한다는 것이죠.
NGCF에서 학습할 때 사용된 feature transformation and nonlinear activation 방법은 효율성에 기여를 하지 않는다는 점을 알아냈음. 그래서 협업필터링에서 neighborhood aggregation과 같이 필수적인 요소들을 포함한 LightGCN을 제안합니다!
그래서 무엇을 할건가 ?
(1) feature transformation and nonlinear activation 가 효과가 없다는걸 증명할거임.
(2) 굉장히 심플해진 LightGCN을 제안할거임.
(3) technical and empirical perspective으로 NGCF와 비교를 할거임.
2. PRELIMINARIES
2.1 NGCF Brief

2.2 Empirical Explorations on NGCF
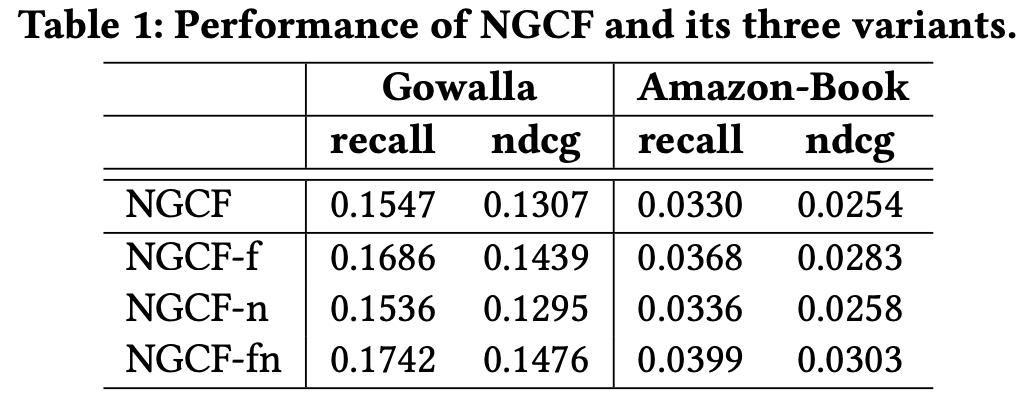
히든노드라 불리는 가중치를 제거하거나 활성화함수를 제거하거나 둘 다 제거했을 때를 보면 둘 다 제거했을 때 가장 성능이 좋은걸 볼 수 있죠?
성능에 있어서 오히려 필요 없다는 걸 잘 보여주죠? feature transformation, activation function의 불필요함을 실험을 통해서 여실히 보여주고 있죠?
3. METHOD
3.1 LightGCN
먼저 GCN 그래프에 특징을 스무딩함으로써 노드의 임베딩을 만들어가는 거죠. 스무딩한다는거는 convolution을 반복적으로 수행하면서 이뤄지구요.
이 반복수행이라는거는 결국 타겟노드의 임베딩을 위해 이웃을 계속 aggregating하는 것이라 볼 수 있구요.
아래식에서 보면 AGG가 aggregation function 한다고 보시면 되겠습니다. 이런 반복수행에 있어서도 뭐 weight를 줘서 weighted sum을하거나 LSTM을 접목하거나 하는데 전부 feature transformation 이랑 activation function을 포함하고 있습니당! 이게 어쨌거나 추천에 있어서 사용자 입력이 스파스하기도 하고 별로 시멘틱하지도 않으니까 이 도메인에서는 잘 안된다는건 확실하다고 말하네요.
⚠그래서 LightGCN이 뭐냐??
아래의 그림은 NGCF에서 보던거랑 비슷하다고 할 수 있는데요. 아래 그림의 설명을 그대로 해석하면 이해가 좀 잘 될거에요!
"Figure 2: An illustration of LightGCN model architecture. In LGC, only the normalized sum of neighbor embeddings is performed towards next layer; other operations like self-connection, feature transformation, and nonlinear activation are all removed, which largely simplifies GCNs. In Layer Combination, we sum over the embeddings at each layer to obtain the final representations."
-> 의역 : "오직 이웃 임베딩들의 normalized sum으로 다음 레이어로 진행된다. self-connection, feature transformation, nonlinear activation은 전부 제거되어서 GCN이 정말 가벼워졌죠? 마지막 임베딩을 만들기 위해서 각 임베딩을 weighted sum하면 된다."

3.1.1 Light Graph Convolution(LGC)
간단한 가중합을 수행하죠. featurte transformation, nonlinear activation을 사용하지 않고 말이죠! GCN에서 했던 정규화는 convolution을 거치면서 스케일이 터지는걸 막아주죠! 바로 아래 식 (3)처럼 말이죵. 뭐 L1놈 같은 방법도 있긴합니다만 이 symmetric normalization이 실험해보니까 성능이 좋다고하네요.

self connection같은 타겟노드 그자체를 통합하지 않고, 이웃들만 사용합니다.
LGNC아키텍처 젤위에를 보면 layer combination operation이 있는데 요게 self connection과 같이 작용이 되니까 NGCF와 달리 생략이 쌉가능합니다.
아래는 NGCF의 아키텍쳐를 캡쳐해온 건데 비교해 보세요. 어때요? 뭔가 해야할게 많죠? 그래서 이번 논문이 좀 더 간단하게 느껴질 수도 있을겁니다.

3.1.2 Layer Combination and Model Prediction
LGCN에서! 유일한 학습이 되는 파라미터는 0번째에 존재하는 임베딩들이다. 계속 Normalized Sum만 해주니까 정작 업데이트 되는 파라미터는 그림에서 보면 $e_{u}^{0}$, $e_{i}^{0}$ 두개를 말한다.

(4)번식은 식(3)에서 봤던 임베딩 K번 더해나가는 걸 의미하는데, 하이퍼파라미터 알파가 들어가 있다. 알파는 1/(K+1)이 좋대요~.~ 불필요한 리소스를 줄일건데 뭐 이 알파를 최적화하면 또 복잡해지니까 뺐습니다.
아마 분모가 계속 커진다는거는 멀리떨어진 이웃에 대한 가중치를 줄이겠다는 것으로 보임.
직관적으로 실험해보고 괜찮아서 픽스한거같음. Layer combination을 만들때 3가지 의미가 포함되어 있죠.
(1) 레이어의 개수가 증가함에 따라 임베딩은 과도하게 스무딩되어버려서 그냥 심플하게 마지막 레이어를 사용하는건 문제의 소지가 있죠.
(2) 다른 레이어들로 부터 나온 임베딩은 서로 의미가 다르죠. 각각 레이어마다 강조되는 의미가 다르기 때문에 weighted sum을 해주는거죠. 첫번째레이어에서는 당장 사용자와 아이템간의 상호작용에 초점을 맞추고, 두번째레이어에서는 공통으로 포함된 다른사용자(아이템)은 누군가에 대해 초점을 맞추고 세번째레이어에서는 또 더 고차원적인 의미를 담을 테니까요. NGCF에서는 concatenate를 하거든욤.
(3) weighted sum으로 다른 레이어에서 나온 임베딩을 결합하는 순간! GCN에서 사용했떤 self-connection과 함께하는 graph convolution의 효과를 얻을 수 있다는거죠.(self-connection을 따로 할 필요가 없다는거죵.)

(5)번식으로 예측값을 만들어서 성능을 평가하면 되겠죠.
3.1.3 Matrix Form

식(6)을 보면 예전에 NGCF 코드 뜯어볼때가 생각이 나죠? 사용자x아이템 매트릭스를 저런 형태로 만들어 놓고 행렬연산을 쉽게 하던 때가 생각나죠?
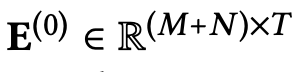
처음 임베딩의 모습은 사용자와 아이템 모두 각각 T차원의 임베딩으로 시작합니다.

식(7)을 보면 앞뒤로 루트씌운 대각행렬을 곱하는 이장면 이것도 어디서 많이 보던게 기억나죠? (참조) 다시 상기해보면 (D)diagonal matrix는 각 노드의 연결중심정도를 나타내죠. 사용자의 경우에는 몇명의 사용자랑 co-accurrence가 있냐를 나타냅니다. 아이템의 경우도 마찬가지고요.
암튼 이 라플라시안 행렬을 곱해주면 가장 큰 특징은 노드간의 연결, self 정보를 계속해서 잊지말고 들고 가는거라고 생각합니다. 여러분의 생각은?
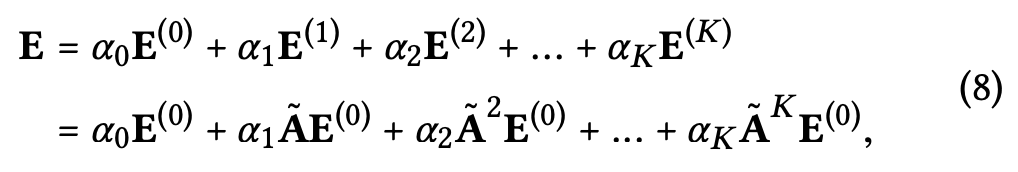
식(8)에서 가장 큰 차이는 초기 임베딩 행렬이 고정된채로 A만 곱해지는 부분입니다. A는 일종의 추정치라고 할 수 있겠는데 밑에 처럼 우리가 처음에 사용자x아이템으로 얻을 수 있는 D(대각행렬)와 A(인접행렬)로 추정할 수 있습니다.
라플라시안행렬은 그래프에 대한 정보를 꾸굮 눌러담고 있죠. 그리고 애초에 라플라시안은 2차 편미분값을 의미하며 우리가 알고 있는 gradient의 의미를 가지고 있어요. 그래서 이를 제곱하고 한다는 것은 계속해서 각 노드의 특징을 곱해주는 것이고, K번 반복한다는 것은 더 많은 이웃을 고려하는 것이죠. K번 곱하면서 계속 나의 이웃의 이웃의 이웃의 이웃의 정보도 조금씩 더 담겨지게되기 때문이죠. 정확하게 K번 곱하는게 K번째 이웃까지 고려하겠다라는 뜻은 아는데.... 모르겠습니다.
아무튼 식(8)은 기존 보다 훨씬 간단한 형태로 최종 임베딩 값을 얻어낼 수 있습니다.

3.2 Model Analysis
3.2.1 Relation with SGCN
2021년 논문 와우. 그래프로 하는 추천알고리즘은 대부분 최신이네요. 아무튼 식(9)는 SGCN에서 제안한 임베딩 과정을 의미합니다.
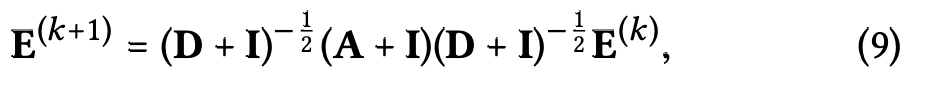
식(10) 에서 I 는 self-connection을 포함하기 위해 사용되는 것이고요. LGCN의 Layer combination과 거진 같다고 해요.

3.2.2 Relation with APPNP
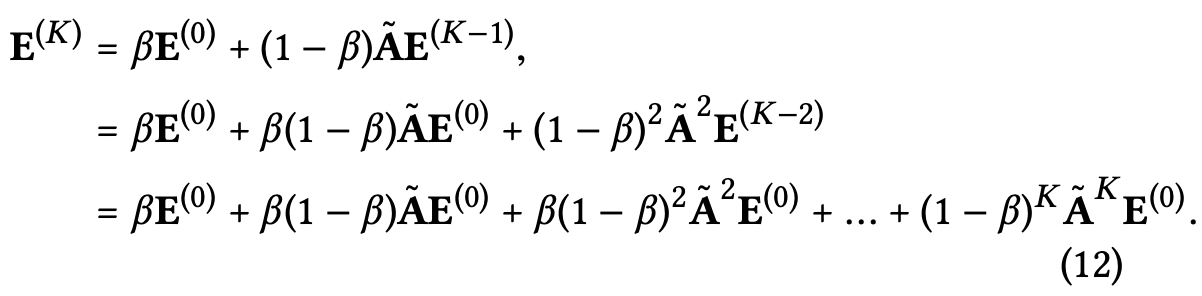
선형성이랑 간결성의 장점으로 뭔가 smooth embedding을 어떻게 하는지로 더 많은 인사이트를 알려주려고 합니다.
식(13)은 사용자 u의 임베딩 표현을 나타내는데, i가 v로 보여지는 부분이 있는데, 사용자가 평가한 모든 아이템들의 집합에서 사용자 u와 동시평가한 사용자의 아이템이 고려되어 진다고 볼 수 있어요.
여기서 사용자 v의 smoothness strength를 사용자 u와의 동시평가 정도에 따라 coefficient로 표현할 수 있습니다. 식(14)처럼 말이죠.


(1) 동시 평가항목이 많을수록 커져요.
(2) 사용자 u가 평가한 아이템이 다른 사용자들로부터 인기가 적을수록 커져요.
(3) 사용자 u에 대한 사용자 v의 활동이 적을수록 커져요. -> 유니크한 환경에 더 가중치를 주겠다는 소리로 들리죠.
*smooth embedding 한다는건 임베딩에 homomorphism을 사용한다는 걸로 보이는데, gradient와 같이 정보를 함축할 수 있다고 보면 되..ㄹ까? 호모몰피즘=(추상대수학에서 준동형(準同型, 영어: homomorphism) 또는 준동형 사상(準同型寫像)은 두 구조 사이의, 모든 연산 및 관계를 보존하는 함수이다.)
3.3 Model Training
학습하는 파라미터는 초기 임베딩 뿐이며, 계산복잡도는 기본적인 MF와 같다고 함.
loss는 BPR을 사용하는데 이건 관측되지 않은 피드백에 대해 예측력을 올려줄 수 있음! 식(15)에서 보면 람다가 달린 초기 임베딩을 정규화한 부분이 있는걸 확인할 수 있음 (L2norm). 그리고 sumation을 차례로 보면 모든사용자들 + 사용자가평가한항목 + 사용자가평가안한항목을 돌면서 loss를 구한다.
BRP로 인해서 각각 사용자마다의 아이템매트릭스가 존재하니 계산량이 크다고 할 수 밖에 없다.
계산량에 비해서 학습이 잘되니까 사용하는 거라고 생각함. 드롭아웃에 대한 설명은 생략한다. feature transformation을 생략하니 즉 W가 없으니까요.

*BPR(Beysian Personalized Ranking)(참조): 사후확률을 최대화 하는 파라미터를 찾는 방법!! implicit feedback을 제시한 가정을 토대로 사용자 별로 아이템의 선호도를 추정해 아이템 랭킹을 매기겠다는 뜻. implicit feedback은 보통 바이너리로 들어오기 때문에 평가하지 않은 아이템들에 대해서는 싫어하는건지 아니면 뭐 아직 경험을 안한건지 알 수 없기 때문에 이문제를 풀어야하는데 이를 해결하기위한 방법론으로 BPR을 사용한다고 보면 될 거같다. 아래처럼 모든 유저 5명의 피드백 정보를 통해서 각 사용자들에게 아이템 랭킹을 모두 매길 수 있게 된다.

4. EXPERIMENTS
4.1 Experimental Settings
-데이터셋

4.1.1 Compared Methods
Mult-VAE라는 방법과 GRMF 방법론 두 개와 함께 비교한다. 파라미터 추정부분 loss function부분에서 차이가 있다.
4.1.2 Hyper-parameter Settings
레이어마다 들어갔던 알파 값은 앞서 설명을 했었고, 임베딩 사이즈를 64로 했다고 한다. 데이터마다 미니배치 사이즈를 소개하고, 전형적으로 1000 에포크를 돌렸다고 한당. 레이어는 1~4개까지 겹쳐보았고, 3이었을 때 성능이 가장 좋았다고 한다.
4.2 Performance Comparison with NGCF
응~ 내가 연구한게 NGCF보다 더 좋아~의 집약체 그잡채~

4.3 Performance Comparison with State-of-the-Arts

4.4 Ablation and Effectiveness Analyses
layer combination을 한거랑 안한거랑 비교하는데 LightGCN-single이 안한거를 의미한다. 레이어를 4개 쌓았을 때 성능이 안좋아지는 경향을 확인해 볼 수 있다. 반대로 했을 때는 Layer combination의 효과로 over-smoothing 문제를 잘 해결했다고 볼 수 있다. 아마존 데이터 같은 경우에는 layer combination을 안한게 성능이 더 좋은데, 알파값 튜닝을 통해서 극복할 수도 있을 것이라함!

normalization schemes를 달리해보며 실험한 결과를 보여줍니다. target node와 neighbor node의 coefficient에 모두 주는 것이 가장 나은 결과라고 합니다.


사용자의 이웃과의 상호작용을 활용하는 smoothing strength는 앞서 설명했다. 이게 본 연구의 핵심이라고 할 수 있다. MF와 비교했을 때, 사용자/아이템 임베딩 모두 smoothness loss 가 낮은 걸로 확인이 된다.

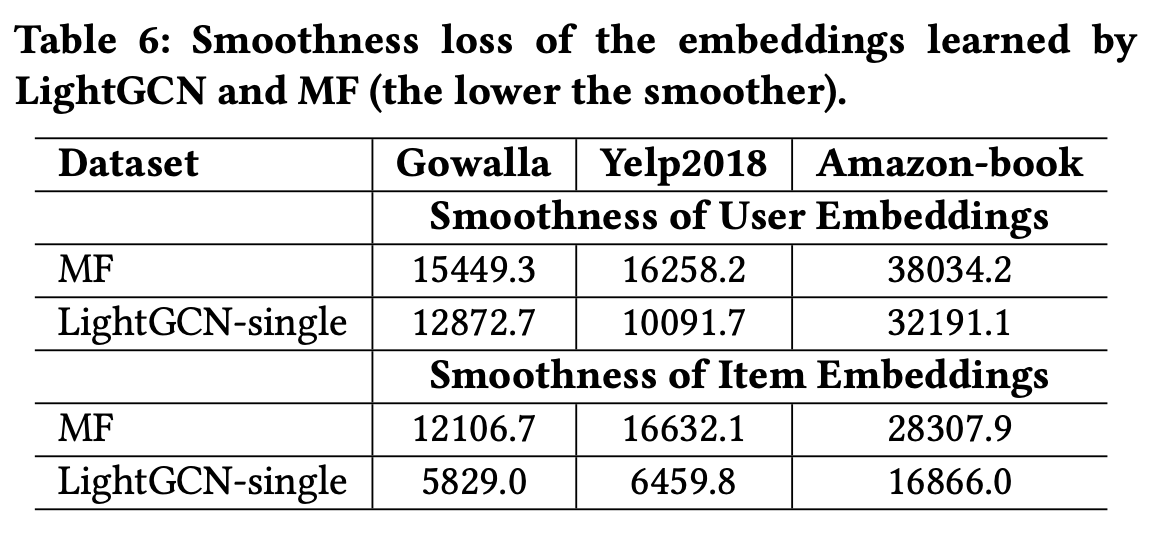
4.5 Hyper-parameter Studies
L2 norm의 하이퍼파라미터 람다 값이 가장 중요한 튜닝 요소다. 람다가 0일 때도 두 데이터셋에 대해서 좋은 성능을 보이는걸 확인할 수 있다. 물론 최적의 성능을 내는 것은 아니지만 굳이 과도한 최적화를 하는 것은 그리 추천하지 않는다고 한다. 즉, 튜닝을 많이 하지 않아도 효율적으로 사용할 수 있다는 것이다.

5. RELATED WORK
5.1 Collaborative Filtering
CF 유명하죠? 근대 추천 시스템에 있어서 말이죵. 아이템, 사용자 임베딩을 파라미터로 업데이트하는게 흔한 패러다임이고 이를 위해서 Matric Factorization이 등장했구요.
이어서 신경망을 가져와서 NCF 같은게 등장했구요, 이런것들은 모델의 상호작용을 강화시켰죠. CF 방법같은 경우에는 과거 정보를 고려했죠. 그리고 이걸 학습할 때 target 값으로도 사용했구요. 게다가 이미 존재하는 아이템의 피쳐들을 가지고서 사용자를 더 잘 임베딩하게 되는 상황까지 이어졌습니다.
SVD++같은 경우에는 아이템의 가중평균을 가지고 사용자 임베딩의 타겟값으로 사용하기도 하구요. 최근에 연구자들은 이러한 아이템의 피쳐가 사용자의 취향을 반영하는데 다양한 기여를 한다는 것을 깨닫게 되었습니다.👏👏
지금까지 어텐션 메커니즘이 이러한 부분을 해결하기 위해 소개되곤 했죠. ACF, NAIS와 같은 것들은 자동적으로 과거 아이템의 중요성을 자동으로 학습합니다. 사용자-아이템의 상호작용에 대해 다시 들여다 봅시다.
즉 로컬 이웃을 인코딩하는데 도움을 줄 수 있고, 결국 이는 임베딩학습에 도움을 주게 됩니다. >>> CF 협업필터링은 사용자와 아이템의 상호작용, 사용자 정보, 아이템 정보 등 과거 히스토리 데이터에 기반함.
5.2 Graph Methods for Recommendation
사용자-아이템 그래프 구조를 통해 추천을 하는 방법이 있습니다. 이전에 ItemRank와 같은 연구는 그래프에 사용자 선호를 직접적으로 전파하기 위한 (label propagation mechanism)라벨 전파 메커니즘을 사용하는데, 얘는 유사한 라벨들을 가지는 노드를 연결하는 것에 초점을 맞춥니다. GNN이 나왔죠. 얘는 임베딩학습을 위해 특히 high-hop neighbor로 그래프 구조를 모델링하는데 한줄기 빛을 선사하게 됩니다. 🌞
최근 연구에서 convolution 접목 모델이 나오는데 Laplacian eigen-decomposition 과 Chebyshev polynomials라는 계산비용이 많이 들어가는 방법이죵. 그런다음 GraphSage, GCN이 다시 정의 됩니다. 이웃같은거를 aggregating 해서 임베딩 할 수 있는 spatial domain에서 재정의 됩니다. 해석이 가능하고 효율이 좋아서 널리널리 쓰이게 됩니다.
이런 Graph convolution의 장점에 따라서 NGCF, GC-MC, PinSage는 GCN을 선택하죠. 사용자-아이템 상호작용 그래프에서 high-hop 이웃으로 추천을 해서 CF signal을 잡아내기 위함입니다. GNN에 대해 죽죽 설명한 것은 결국 LightGCN이 탄생하는데 깊은 인사이트를 주기 때문에 옴총 가치가 있다고 할 수 있슴당.
LightGCN은 이런 방법들에 비해 계산량도 줄였고, 거진 MF만큼 간단하게 모델링에 성공했슴다! 축하축하..
6. CONCLUSION AND FUTURE WORK
정리를 해보겠습니다.
이 논문에서 주요 방법은 graph convolution을 간결하게 고쳤고, layer combination을 사용했습니다.
- light graph convolution -> feature transformation, nonlinear activation을 지웠다. >>> 간결한 모델을 만들 수 있게됨.
- layer combination -> 마지막에 모든 레이어에서 나온 임베딩을 weighted sum한다. >>> self-connection의 효과를 얻을 수 있고, oversmoothing되는걸 방지할 수 있다.
'추천시스템' 카테고리의 다른 글
| GC-MC(Graph Convolutional Matrix Completion) (0) | 2023.02.20 |
|---|---|
| 추천시스템. 염두에 둘 것. (0) | 2022.11.20 |
| 추천시스템 기술 요약 (0) | 2022.11.13 |
| 딥러닝과 추천시스템 (0) | 2021.03.18 |
| Model based Collaborative Filtering (0) | 2021.02.04 |



댓글