Abstract
본 논문에서는 평점 행렬의 빈공간을 채우는 Completion 관점에서 바라보고 있습니다. 영화 평점 행렬과 같은 데이터를 그래프 기반으로 바라보면서 값을 채우는 식으로 추천을 하게 되는데요. 기존에 알고 있던 Matrix Factorization과 결이 같다고 볼 수 있습니다.
영화 평점 행렬같은 케이스를 bipartite graph로 보는데 아래의 사진과 같이 빨간색은 사용자, 파란색은 영화. 이렇게 생각하면 됩니다.
GC-MC는 일반적인 CF 벤치마크에 대비 경쟁적인 성능을 보인다고 합니다.

1. Introduction
본 논문에서는 행렬 완성(completion)을 그래프의 링크를 예측하는 문제로 봅니다. CF는 사용자와 아이템 간의 이분 그래프로 나타낼 수 있기 때문입니다. 그래서 사용자가 평가한 아이템을 예측하는 문제는 곧 사용자에서 아이템으로 뻗는 링크를 예측하는 것으로 볼 수 있습니다.
본 논문에서는 사용자와 아이템간의 관계를 통해 auto-encoder로사용자와 아이템에 대해 latent feature를 생성합니다. 생성한 latent feature는 bilinear-decoder를 통해 예측값을 출력하게 됩니다.
여기서 사용자가 가리킬 아이템의 링크를 맞추는 것처럼 문제를 풀면 추천시스템의 고질적인 문제인 콜드 스타트 문제에 도움을 줄 수 있습니다.
2. Matrix completion as link prediction in bipartite graphs
아래의 그림에서 $M$은 사용자와 아이템의 평점 행렬을 의미합니다. 평가하지 않은 항목에 대해서는 BPR loss를 사용할 때처럼 랭킹을 굳이 매긴다던지 하지 않고, 0으로 처리하는 것을 볼 수 있죠.
Bipartite graph에서는 사용자와 아이템을 연결하는 링크와 사용자의 평점도 함께 달려 있는 것을 볼 수 있습니다. 이런식으로 그래프와 같이 표현합니다.
GC-MC모델을 통한 순전파로 사용자와 아이템의 latent feature인 $U, V$를 생성합니다. MF에서 latent feature를 만들어내는 과정과 동일하게 진행합니다. 그리고 마지막 평점을 뽑아낼 때 내적을 사용해서 만들었다면 여기서는 bilinear-decoder를 활용해서 예측값을 뽑아낸다고 보시면 됩니다.

2.1 Graph auto-encoders
여기서는 오토인코더의 인코더와 디코더에 대해 정의를 합니다. 크게 두가지로 정의하는데 Graph Encoder모델과 Pairwise Decoder모델 이 두가지로 정의합니다.
먼저 Graph Encoder는 $Z = f(X,A)$와 같이 정의합니다. 함수 $f$에 입력으로 들어가는 $X$는 사용자x아이템 크기의 행렬로 그래프기반 행렬을 구성할 때 늘 등장하는 형태의 행렬이네요. $A$는 인접행렬로 서로 어떻게 연결이 되어 있는지 연결 정보를 말해주는 행렬입니다. 이를 위해 $Z=f(X, M_{1}, ... , M_{R})$와 같이 각 평점마다 행렬을 구성해서 해당 평점을 가진 쌍에게 0 또는 1로만 체크해서 평점 정보를 갖도록 합니다. 이 과정을 거침으로써 사용자와 아이템의 latent feature를 생성하게 됩니다.
다음 Pairwise Decoder는 $\hat{A} = g(Z)$와 같이 정의합니다. 디코더는 출력을 해주는거니까 최종적으로 평점을 예측하는 값을 출력합니다. 인코더에서 평점별로 존재했던 행렬을 종합해서 사용자와 아이템 사이에 예측평점 값을 얻는 기능을 수행하는 거라고 보면 됩니다.
2.2 Graph convolutional encoder
Weight Sharing은 CNN에서 해당 weight 주변의 정보도 공유할 수 있다는 장점인데 이것이 추천에서도 좋게 사용이 될 수 있어요. 직관적으로 말하면 이웃의 정보를 활용한다는 것이고, 이러한 장점으로 gnn에서 gcn이 각광을 받았던 것입니다.
Local Graph Convolution는 message들이 그래프 상에서 message passing되는 형태를 말합니다.

식(1) 에서 본 논문에서 말하는 message $\mu$의 개념을 설명할 수 있는데, 사용자와 아이템 $i, j$가 평점 $r$로 연결되어있는 것을 말합니다. 식에서 $u_{j \rightarrow i,r}$ 가 그것입니다. $c_{ij}$는 정규화를 위한 상수이고, $W_{r}$는 평점에 대한 weight를 의미합니다.

식(2)는 인코더를 통해서 히든레이어가 생성되는 것을 의미합니다. 정확히 말하면 Graph Convilution Layer ! 이어서 $accuum$은 수식들을 다 종합한다는 것을 의미합니다. $\sigma$는 활성화함수를 의미합니다.

2.3 Bilinear decoder
디코더 부분에서 예측평점을 출력한다고 했는데, 보통 사용자와 아이템 벡터의 내적으로 예측평점을 뽑아냈다면 여기서는 아래와 같이 softmax 함수로 뽑아내게 됩니다. $Q_{r}$은 $E \times E$ 차원의 학습가능한 파라미터 행렬입니다.

그리고 뽑아낸 확률을 가중치로 활용해 가중평균으로 최종 예측 평점 행렬을 계산합니다.

2.4 Model training
loss: negative log likelihood를 최소화하는 방향으로 학습을 진행하네요. $k=l$인 경우에는 $I[k=l] = 1$이 되고 그렇지 않은 경우에는 0을 줍니다. 이는 관측되지 않은 값에 대해서 mask를 씌운다고 보면 됩니다. 예측평점과 실제평점을 고려할 때 실제 평점이 없으면 loss를 구할 수 없기 때문입니다.

Node dropout: 식 (3) 히든레이어에 적용했다고 합니다.
Mini-batching: 미니배치는 여러 장점이 있죠! GPU의 스펙이 딸리거나 혹은 일반화에도 기여를 할 수 있죠.
2.5 Vectorized implementation
행렬을 활용해서 벡터 연산을 효율적으로 수행하기 위한 친절한 수식 설명! 식 (8)이 식(2)와 유사하다고 합니다.

2.6 Input feature representation and side information
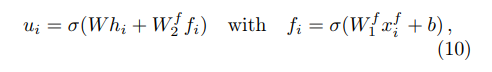
그래프 기반 방법에서 입력으로 정보가 별로 없는 sparse 한 벡터를 넣어버리면 병목현상이 발생한다고 합니다. 그래서 사이드 정보를 활용한다고 합니다. 그렇기에 위 식(10)에서 $f_{i}$를 사용해 사용자 $i$의 부족한 정보를 메꿔주도록 합니다. 부족한 정보는 얼마없는 평점이 되고, 사이드 정보는 사용자의 데모정보 같은 정보들이 있을 거에요!
5. Conclusions
MF와 같은 matrix completion 문제를 해결하기 위해 그래프 기반의 아이디어를 도입하였고, 이를 오토인코더 형식의 아키텍처로 풀어내었다.
실제로 코드를 돌려보지는 않았지만... 실제 빅데이터에서는 MF도 상당히 메모리를 많이 잡아먹는데 이 방법은 어떨지 궁금한데요. 실제로 그래프 기반의 방법들이 추천성능에 SOTA를 기록하고 있는 만큼 계산성능과 콜드스타트의 문제를 더 효과적으로 커버할 수 있다면 가히 좋은 알고리즘이라고 탕탕탕! 하고 써먹어도 좋을 것 같다는 생각이 듭니다~ 👏
'추천시스템' 카테고리의 다른 글
| LightGCN (0) | 2023.02.12 |
|---|---|
| 추천시스템. 염두에 둘 것. (0) | 2022.11.20 |
| 추천시스템 기술 요약 (0) | 2022.11.13 |
| 딥러닝과 추천시스템 (0) | 2021.03.18 |
| Model based Collaborative Filtering (0) | 2021.02.04 |



댓글