최적화 문제를 풀기 위해서 GD(Gradient Descent) 방법으로 최적의 해를 찾는다는 것을 들어보았을 것이고, 이 gradient는 소위 기울기라 알려져 있다. 이 gradient는 미분을 통해 쉽게 얻는다는 것도 알고 있다. 벡터, 행렬의 미분으로 가면 더 복잡해 지지만 다항식에 대한 미분은 어렵지 않게 구할 수 있다. 이번 장에서는 머신러닝에서 미지수가 하나인 univariate function 에 대한 내용을 알아본다.
머신러닝 알고리즘을 접하다 보면 자연스레 최적의 parameter값을 찾는 문제에 직면하게 된다. 이렇게 최적의 값을 찾아가는 과정을 learning이라고 한다. 이 과정에서 필요한 정보가 gradient 이다.
Vector Calculus
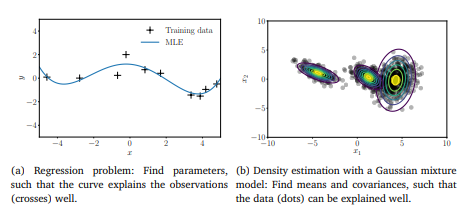
(a) 와 같은 경우는 + 모양의 관측치를 잘 설명해줄 수 있는 최적의 그래프를 구해주어야 한다. 이러한 함수를 likelyhood라는 함수로 정의하고 이를 최대화하는 과정을 겪어서 파란색 선과 같은 최적의 curve를 가지게 된다.
(b) 여러개의 가우시한 혼합 모형으로 밀도를 추정하게 되는데, 여기서도 얼마나 데이터를 잘 설명하는가를 측정할 수 있는 likelyhood를 정의하고 이를 최대화하는 mean과 covariance를 측정하게 된다.
이러한 최적화과정에서 목적함수의 gradient를 찾아나서야 한다.

함수의 개념은 $f: \mathbb{R}^{D}$ $\rightarrow$ $\mathbb{R}$ 처럼 $D$차원의 벡터를 input으로 받아 스칼라 값으로 매핑하게 되고, 이미 알고 있는 정의역, 공역, 치역의 개념을 떠올리면 이해하기 쉽다.
이번 장에서는 함수들(differentiable)의 gradient(gradient poing: direction of steepest acsent)를 구하는 방법을 배운다.
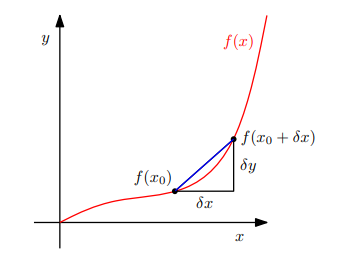
아래의 이미지를 통해서 x가 변화할 때 y의 변화량 즉, 아래의 식 (5.3)과 같이 나타낸다.
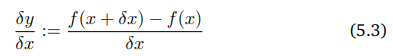
아래의 예제는 polynomial 에 대한 미분을 하는 과정을 나타낸 것이다. (5.6d)을 보면 공식처럼 외우고 있던 방법을 떠올리게 된다.


Definition 5.3은 $k$번의 미분으로 얻은 polynomial을 approximation하는 그래프들은 차수를 높일수록 특정 $x$에 대하여 설명을 잘 하게 된다. 여기서는 $x = 1$일 때는 기준으로 구한 것이기 때문에 그 주변에 대해서 approximation이 이루어 진다.
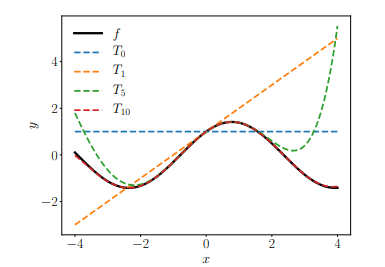

예제 5.3은 6번의 미분을 통해 원래의 $f(x)$와 같아지게 됨을 보이게 된다.
아래의 식들은 기본적인 미분공식이다. 특히 Chain rule의 경우 이후에 많이 쓰인다.
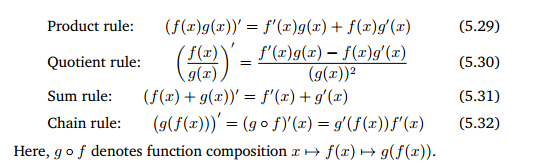
아래의 예시는 간단한 Chain rule을 풀어보는 것이다.

(5.32)를 그대로 적용하되 $h(x)$를 두 함수로 표현하는 것에 주의하자. 이후에 전개는 그대로 따라하면 아래와 같이 $h(x)$의 미분값을 구할 수 있다.

지금까지 univariate variable에 대한 미분을 했다면 이제는 mutivariate variable $x \in \mathbb{R}^{n}$에 대한 미분을 한다. 여기서 gradient를 구하는 방법은 여러개의 variable중 하나씩에 대한 미분을 진행하고 모두 모아주면 된다. 이 모아진 것을 gradient라고 하게 된다. 그리고 특정변수에 대한 gradient를 partial derivative라고 한다.

식 (5.39)는 하나씩 변수들에 대한 미분을 진행하고 이들을 모아놓은 것이 (5.40)이 된다. 이를 $f$의 gradient라고 한다.
아래의 예제 5.6은 각각 $x, y$ multivariate variables에 대한 Partial Derivatives를 구한 것이다.


이번엔 mutivariate variables의 Gradient를 구해보자.

이 위의 예제에서도 partial derivatives를 구했는데, 여기서도 마찬가지로 구하고, 이들을 모은 로우 벡터 형태로 만들어 주면 된다.
아래는 Partial derivatives의 기본적인 규칙에 대한 설명이다. 순서에 주의하여야 한다.


Chain Rule에 대해서 살펴보자. 여기서는 $x_{1}과 x_{2}$역시 $f$처럼 함수라고 한다. 이때 $t$라는 하나의 input을 받아서 2개의 output이 탄생하였고, 이 둘을 $f$함수를 거쳐 하나의 output을 내게 되었다. 다시 말하면 $t$라는 input은 두 개의 함수를 만나 각각 $x_{1}(t), x_{2}(t)$ output을 발생시키고, 이게 다시 2개의 input으로 multi variative function인 $f$를 만나서 $f( x_{1}(t), x_{2}(t) )$ 가 되어 최종적으로는 1개의 output이 된다는 말이다. 그래서 $f$에 대한 $t$를 미분하여 gradient를 얻는 것이다.
output이 여러개일 경우 gradient를 column vector로 나타내주고, 한개일 경우 이전 처럼 row vector형태로 나타내주면 된다. 계산 순서에 유의하자.

아래의 식 3개는 위에서 처음 input이 $t$로 하나였지만 이번에는 $s$와 $t$로 두개로 시작한다는 점이 다를 뿐 다른건 다 같고, 일반화를 표현한 것이다.
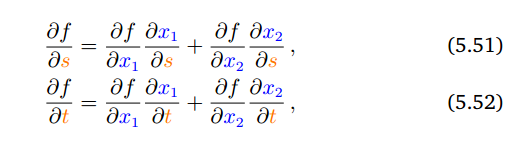

지금까지 $\mathbb{R}^{n}$을 real value로 매핑하는 함수를 미분하였는데, 지금부터는 real value가 아닌 $\mathbb{R}^{m}$으로 매핑하는 함수를 미분한다. 즉 미분 값이 vector형태로 나오는 함수를 미분한다.

이전과의 차이는 $f$가 총 $m$개가 있어서 각각의 gradient값을 뱉어낸다는 점이다.
아래는 맨처음 partial derivatives를 할 때 봤던 식인데, 이거를 함수 $f$의 개수만큼 열벡터로 죽 나열해준것이다.
최종적으로 네모칸이 의미하는 것은 $m$개의 함수를 하나의 변수$x_{1}$로 미분한 값이 되고, 행렬의 로우는 각 함수의 gradient값이다.

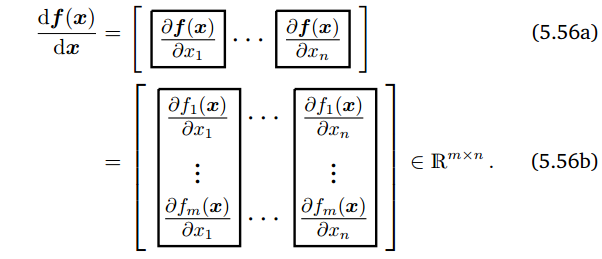
row로 죽 나열된 것이 함수의 output이 되고(gradient), col방향으로 죽나열된 것이 input이 된다.
이 매트릭스를 Jacobian이라고 한다.
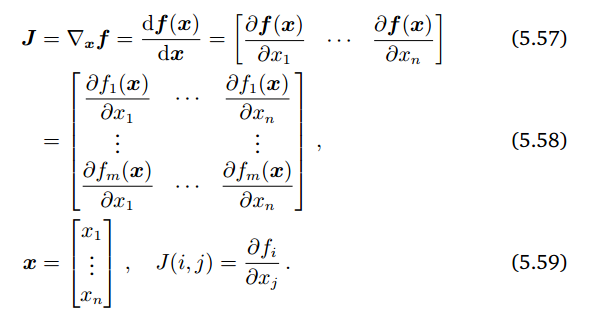
linear mapping으로 trasformation했을 때 얼마나 scaling되는지를 나타낼 때 linear trasformation일 때 가능한데 non linear transformation일 경우에는 어떤지 알려주는게 Jacobian이고, 이때 그 볼륨은 approximation이다.

위의 그림처럼 f를 통해 선형맵핑을 한다고 해보자. $b$를 [(1,0), (0,1)], $c$를 [(-2,1),(1,1)] 이라고 하면, 쉽게 transformation matrix가 [(-2,1),(1,1)] 이라는 것을 알 수 있고 이를 식으로 나타내면 다음과 같다.
그리고 이를 partial derivatives 하게 되면, Jacobian을 구할 수 있게 된다. 이에 determinant를 구하면 3을 얻게 된다.


아래의 그림은 우리가 partial derivatives를 하고 난 후에 어떤 shape을 가지는지를 나타내주는 그림이다. 1차원에서 1차원으로 가는 함수의 미분은 real value gradient를 가졌었고, 마지막으로 n차원에서 m차원으로 맵핑하는 함수에 대한 미분은 m x n 차원의 gradient 값이다.

벡터를 다루는 함수에 대한 gradient를 구하는 예제를 살펴보자.
$f(x)$를 $x$에 대해 미분하는 것이고, output이 M 개니까 로우가 M행이 되고, input이 N개니까 column이 N개가 나와야 된다. $f_{i}(x)$값은 $A$의 $i$번째 element와 $x_{j}$와의 dot product라는 사실을 알 수 있다.(5.67)
그래서 최종적으로 M x N 행렬로 gradient가 나타난다.

최종적으로 $f$에 대해 $x$를 미분하면 아래의 Chain Rule로 대입하여 gradient를 구할 수 있다.

아래의 예제 5.11은 회귀분석의 회귀식을 떠올릴 수 있다. 예측치와 실제값과의 loss를 최소화하기 위한 gradient를 찾는 과정이다. 독립변수 $\Phi$ 벡터와, 회귀계수 $\theta$와 실제값(관측치) $y$에 대한 식으로 loss에 대해서 $L_{2}$ norm을 구하고(5.76), 이 $L$을 미분하여 gradient 를 구하고 이를 활용하여 loss를 최소화한다.

다음장에서는 행렬의 gradient를 구해본다.
'수학' 카테고리의 다른 글
| Backpropagation and Automatic Differentiation (0) | 2020.05.30 |
|---|---|
| Gradients of Matrices (0) | 2020.05.27 |
| Linear Algebra(6) (0) | 2020.04.27 |
| Linear Algebra(5) (0) | 2020.04.26 |
| Linear Algebra(4) (0) | 2020.04.26 |




댓글