행렬이 주어졌을 때 행렬을 벡터로 미분한 gradient 혹은 행렬을 다른 행렬로 미분한 gradient 들은 multidimensional tensor로 계산이 된다. 이 gradient를 어떻게 구하는지 알아본다. multidimensional tensor이기 때문에 output의 dimension과 크기만 신경쓰면 지금까지 배운 미분개념에서 크게 벗어나지 않는다.
예를 들어 행렬 $A \ (m \times n)$ 행렬 $B \ (p \times q)$로 미분되면 4 dimensional tensor $J$가 되고, $J_{ijkl}$ 엔트리에는 각각 partial derivatives 값들이 들어간다.
행렬을 벡터 또는 행렬로 미분했을때 output의 shape을 잘 상기해야한다.
$A$라는 행렬을 $x$벡터로 미분했을 때, 최종적으로 4x2x3 의 결과가 되는데, 이 때 각 셀에는 $A$와 $x$의 1 dimension 곱으로 표현된다. 그림을 통해서는$A$ 를 각각 $x_{1}$, $x_{2}$, $x_{3}$ 으로 미분한 partial derivatives들이 있고, 최종적으로 4x3x4 결과가 되는 개념만 파악하자.

위의 그림을 예제 5.12로 보면, $M$dimension의 $f$를 $A$행렬로 미분하면 (5.86)과 같이 $M \times (M \times N)$ dimension의 결과를 얻는다.
(5.87)은 partial derivatives의 벡터들을 모아 gradient를 이루게 된다. (5.88)식은 $A$의 하나의 element에 대해서 어떻게 표현되는지 보여준다. 행렬 $A$의 element들과 $j$번째 $x$ 벡터와의 곱으로 표현된다. 특정 $f_{i}$를 $A_{iq}$ 로 미분하여 $x_{q}$라하고 이는 하나의 행벡터로 partial derivatives가 된다.

특정 $x$를 돌아가면서 미분하기 때문에 나머지는 0이 된다는것을 알고 있다. 그래서 아래와 같이 한 partial derivatives를 표현한다.
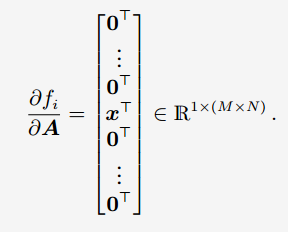
이번에는 행렬을 행렬로 미분하는 예제를 살펴보자.
output의 shape 부터 살펴보면 (N x N) x (M x N) 의 4 dimension tensor라는 것을 알 수 있다. $K$의 각 element들은 $r$의 내적으로 표현된다.

$\partial_{pqij}$ 를 4가지의 경우에 따라서 entry가 나뉜다. 이 관계에 따라 최종적인 gradient 를담고 있는 4 dimension 에 각각의 element로 값을 가지고 있다.
아래의 정리는 gradient 계산에 자주 사용되는 정리이므로 외워두면 좋다.

'수학' 카테고리의 다른 글
| Higher-Order Derivatives (0) | 2020.05.30 |
|---|---|
| Backpropagation and Automatic Differentiation (0) | 2020.05.30 |
| Differentiation of Univariate/Multivariate Functions (0) | 2020.05.27 |
| Linear Algebra(6) (0) | 2020.04.27 |
| Linear Algebra(5) (0) | 2020.04.26 |




댓글