Linear Algebra(5)에서는 Orthogonal projection, determinant, trace 등에 대해 알아본다.

위 그림은 보통 linear regression에서 자주 보던 그래프이다. 원래 파란점들은 이차원 평면이 점으로 표현이 되었지만, 이를 1 dimension으로 의미있는 저차원으로 표현하여 설명을 할 수 있는데 이를 projection이라고 한다.

projection의 정의는 위와 같은데 projection을 다시 한번 수행해도 한번 수행한 것과 같다는 말이다.

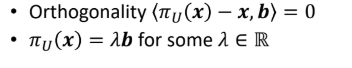
$x$가 n dimension이고, $b$라는 1 dimension에 표현하고자 하여, $x$에서 $b$로 수직으로 내리꽂는 $\pi_{U}(x)-x$를 내려서 표현하게 된다. 수직이라하면은 왜 가장 길이가 짧고 가깝다는 직관적인 의미를 생각하면 이해하기 쉽다. 최단 거리에 내리 꽂아서 최대한 가깝게 표현하겠다는 의도이다.
두가지 성질 중 첫번째는 직교하여 내적이 0이 된다는 것이고 두번째는 projection한 벡터는 결국 $U$ 공간에 있으니까 $U$의 basis들로 선형결합하여 표현가능하다는 것을 말한다.
자 이제 1차원의 subspace로의 projection을 3 step을 통해서 coordinate $\lambda$와 projection $\pi_{U}(x)$ 그리고 $U$에 매핑하는 모든 $x \in \mathbb{R}^{n}$의 matrix $P_{\pi}$ projection을 구하는 식을 알아본다.
1) coordonate $\lambda$ 를 찾아라.
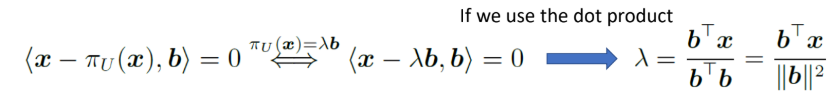
projection한 벡터와 기존의 벡터가 수직이고 이는 내적이 0이란 소리를 이용하여 람다를 구할 수 있다. inner product의 성질에 따라 분배하고 람다에 관해 정리해준다.
2) projection point인 $\pi_{U}(x)$를 구하자.

교환법칙이 되게끔 위치만 바꾸어서 정리해준다.
3) projection matrix $P_{pi}$ 를 구한다.

분모 부분은 scalar가 되고 분자 부분은 n x n 행렬이 되어 결과값이 행렬이 되게 된다. 즉 $U$에 span하는 기저들로 표현이 가능하기 때문에 더이상 $n$개의 coordinate가 필요하지 않게 된다.
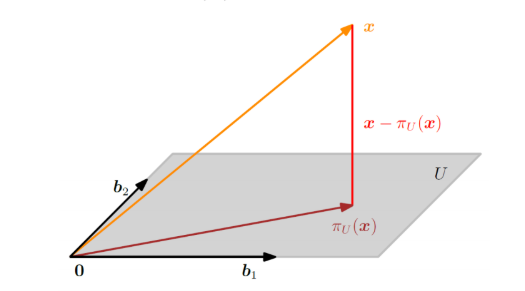
이제 general하게 고차원에서 저차원으로의 projection에 대해 3 step으로 알아보자.
1) 람다를 찾아라.
$m$ dimension의 $U$라는 subspace에 projection한 벡터는 $x - \pi_{U}(x)$ 즉 $x - B \lambda$와 같아 아래의 수식처럼 풀어내게 되면 최종적으로 $\lambda$를 구할 수 있게 된다. 저 식은 마치 회귀계수를 구할 때 보던 정규방정식.. 을 떠올리게 한다.
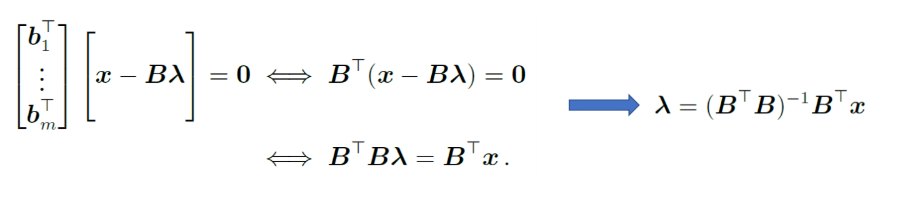
여기서 $B^{T}B$는 full rank로써 invertible해야한다. 역행렬이 존재해야한다.
2) 프로젝션 포인트 $\pi_{U}(x)$를 구하라.

3) 프로젝션 매트릭스 $P_{\pi}$를 구하라.

정리해보면 projection point는 여전히 $n$ dimension에 $U$ 하에 있고, $U$의 기저들로 $m$ 개의 coordinate을 구하여 projection vector를 구하게 된다.

Gram-Schimit orthogonalization은 아래의 예제 처럼 projection point를 찾으면 norm으로 나누어 normal하게 해주고 이 과정을 계속해서 반복해 나가는 걸 말한다.

아래의 그림은 affine space $L$에서 projection을 하는 방법인데 (a)에서 (b)로 넘어갈 때 offset을 빼준 space를 정의하고 원점에 맞춰서 projection을 하고 다시 원래상태로 돌아가서 projection을 해주면 된다.

Determinant and Trace

위와 같이 표현한다.

중고등학교때 역행렬 구할 때 판별식으로 배웠던 그것이다. 행렬 $A$를 하나의 실수값으로 매핑하는 것이다.
이 정방행렬이 upper-triangular matrix이거나 lower-triangular matrix이면 대각원소의 곱으로 determinant가 정의된다.
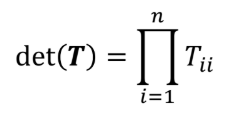
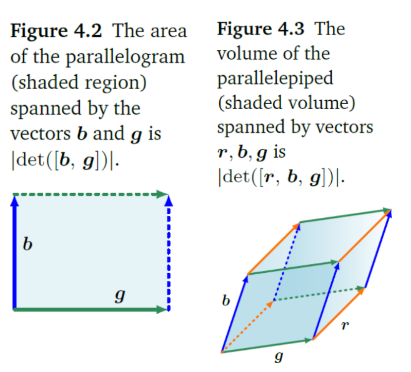
determinamt는 볼륨을 나타낸다고 한다. spanning vector들의 방향을 가리키는 부호정도로 생각하면 된다. 어떤 부피같은 것을 말한다. column vector들이 구성하는 도형의 volume에 해당한다.
역행렬을 구하는 Laplace Expansion 방법.


1행1열 제외한부분에 (1) 곱하기 1,1원소 곱하기 나머지 부분인 (2x2)determinant값 +
1행2열 제외한부분에 (-1) 곱하기 1,2원소 곱하기 나머지 부분인 (2x2)determinant값 +
1행3열 제외한부분에 (1) 곱하기 1,3원소 곱하기 나머지 부분인 (2x2)determinant값 +
2행1열 제외한부분에 (1) 곱하기 2,1원소 곱하기 나머지 부분인 (2x2)determinant값 +
2행2열 제외한부분에 (-1) 곱하기 2,2원소 곱하기 나머지 부분인 (2x2)determinant값 +
2행3열 제외한부분에 (1) 곱하기 2,3원소 곱하기 나머지 부분인 (2x2)determinant값 +
3행1열 제외한부분에 (1) 곱하기 3,1원소 곱하기 나머지 부분인 (2x2)determinant값 +
3행2열 제외한부분에 (-1) 곱하기 3,2원소 곱하기 나머지 부분인 (2x2)determinant값 +
3행3열 제외한부분에 (1) 곱하기 3,3원소 곱하기 나머지 부분인 (2x2)determinant값 = -5 가 나온 것이다.
가우스소거법으로 upper triangular matrix를 만들면 바로 대각원소 곱으로 det를 구해버릴 수 있다.
trace는 대각원소들의 합을 말한다.

아래의 성질은 자명한 사실.
'수학' 카테고리의 다른 글
| Differentiation of Univariate/Multivariate Functions (0) | 2020.05.27 |
|---|---|
| Linear Algebra(6) (0) | 2020.04.27 |
| Linear Algebra(4) (0) | 2020.04.26 |
| Linear Algebra(3)_linear Mappings (0) | 2020.04.07 |
| Linear Algebra(3) (0) | 2020.04.06 |




댓글