저번 장에서 basis와 rank 등에 대해 살펴봤는데, 이제 mapping을 알아볼 차례인데 이부분을 잘 알아야 추후에 matrix factorization을 이해하는데 도움이 된다.
Linear Mappings
초반에 벡터 끼리의 합 혹은 벡터와 스칼라 곱의 결과가 벡터가 나오는 것에 대해 배운 적이 있다. 이런 느낌을 살려 생각해보면 여기서 우리가 원하는 것은 mapping을 할 때 벡터가 가진 속성을 유지하는 것이다. 두 개의 실수 스페이스 $V, W$가 있다. mapping $\Phi : V \rightarrow W$ 는 $V$라는 벡터스페이스를 $W$로 보내주는 역할을 한다. 그리고 벡터 공간의 구조를 보존하게 된다. 아래의 (2.85), (2.86) 처럼. 약간 고등학교 때 배운 합성함수의 느낌이 나기도 한다. $f(a) + f(b) = f(a+b)$ 이었던가.. 하는.

mapping이 function과도 비슷한데 여기서 나오는 '쁴'라고 읽는 $\Phi$라고 하는 맵핑은 우리가 흔히 아는 함수기호 $f$처럼 생각하는게 정신건강에 이로울 듯 하다.
Linear Mapping은 맵핑 중 하나의 케이스인데, vector space $V, W$ 에 대해서 mapping $\Phi : V \rightarrow W$가 linear mapping(vector space homomorphism or linear transformation)라고 부른다.

(2.87)은 Linear mapping을 나타내는데 여기서 $V$에 존재하는 $x, y$와 실수 집합에 속하는 $\lambda, \psi$가 있을 때, 벡터스페이스 $V$에 존재하는 $(\lambda x + \psi y)$를 맵핑$\Phi$ 시킨 결과가 각각 벡터스페이스 $W$에 존재하는 $x$, $y$를 각각 맵핑$\Phi$ 시킨 값들의 linear combination과 같아지면 이러한 맵핑 $\Phi$를 linear mapping 이라고 부른다.

$injective$, $surjective$, $bijective$라 해서 단사, 전사, 전단사 라고 생각하면 된다. 단사라하면 흔히 정의역이 공역에 맵핑될 때 공역의 치역과 일대일로 대응하는 것이고, 전사는 매핑된 공간인 공역과 치역이 같은 것을 의미하고, 전단사는 말그대로 이 둘의 성질을 모두 갖는 것을 말한다.
inverse of $\Phi$라고 하여 $\Psi \circ \Phi(x) = x$ 에서 매핑 $\Phi(x)$한 것에 매핑하여 다시 자기 자신이 나오게 하는 맵핑 함수를 $\Phi^{-1}$ 이라한다.
벡터스페이스 $V$와 $W$사이의 linear mapping의 특별한 케이스를 살펴보자

맵핑이 linear할 때, 전단사 일 때를 기준으로 나뉘어져 있다.
$dim(V) = dim(W)$이면 유한 차원의 $V$와 $W$를 isomorphic하다 한다. 즉 두 벡터스페이스 가 차원이 같으면 둘 사이에는 linear, bijective 한 맵핑이 존재한단 것이다. 다시 말해 동일한 차원(basis 개수)의 벡터 스페이스들은 정보 손실 없이 서로서로 변환이 될 수 있다.
coordinate. 좌표의 정의에 대해 알아보자. 벡터스페이스 $V$ 와 이의 ordered basis $B = (b
_{1}, ... ,b_{n})$ 가 있을 때, $x \in V$ 인 $x$는 $B$에 대해서 unique한 representation을 가지게 된다(2.90). representation은 linear combination이다.
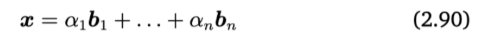

(2.90) 처럼 선형결합에 포함된 상수들을 $B$에 대한 $x$의 coordinate라고 한다. (2.91)은 ordered basis $B$에 의해 정의되는 coordinate vector 또는 coordinate representation이라 한다.

그림 2.8은 동일한 차원의 한 벡터가 $e$, $b$라는 기저를 각각 가질 때 똑같은 좌표 $x$를 만들기 위해 서로 다른 coordinate가 필요하다는 것을 보여준다. basis change에 대한 내용은 후에 다루게 된다.
Transformation Matrix. 벡터스페이스 $V, W$에 각각 대응하는 ordered basis $B=(b_{1},...,b_{n}), C=(c_{1},...,c_{m})$가 있고, mapping $\Phi : V \rightarrow W$ 있다. $j \in \left \{ 1,...,n \right \}$ 일때, $C$에 의해 정의되는 $\Phi(b_{j})$의 unique한 표현으로 아래와 같이 나타낼 수 있다.
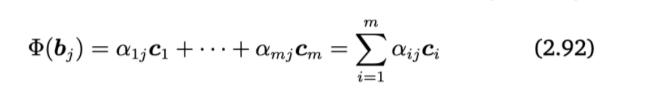
이를 $transformation matrix$ $A_{\Phi}$라고 하며 이 원소들은 아래와 같다.


예제를 보면 transformation matrix가 어떤건지 직관적으로 알 수 있다. 2.95의 식처럼 $V$의 기저들을 C 의 기저의 선형결합으로 표현하며, 이 때, coordinate값을 가지고 2.96의 행렬로 표현하게 되고, 이 행렬이 곧 transformation matrix이다.

transformation matrix $A_{1}, A_{2}, A_{3}$는 a에 있는 기존의 2차원 벡터 집합을 각각 b, c, d로 transformation 한다. transformation matrix를 사용하면 쉽게 행렬을 변환할 수 있다.
basis change.

기저 변환(basis change)을 하는 이유는 기존의 basis로 transformation matrix를 구할 때보다 단순한 형태로 만들 수 있다.
위 그림의 왼쪽은 $B$에서 $C$로 transformation 할 때 변환을 해주는 행렬 $A_{\Phi}$를 구하는 것을 오른쪽에 $B, C$의 각각 다른 기저 사이에서의 변환을 위해$\tilde{A_{\Phi}}$ 행렬을 구하고 싶다는 것이다.

위의 예제는 왜 basis change를 해야하는 지를 알려준다. 기존의 $B$에서의 canonical basis(표준기저) 인 ([1 0], [0 1])로 transformation matrix A를 구한 결과 (2.100)과 같이 구했고, 후에 canonical basis 가 아닌 새로운 basis 인 ([1 1], [1 -1])를 가지고 transformation matrix를 구하면 $\tilde{A}$와 같이 기존의 $A$보다 간단한 형태의 transformation matrix를 구할 수 있다는 것을 말해준다.

(2.105)의 식으로 우리는 새로운 transformation matrix를 구할 수 있게 되는데,

(2.105)를 그림으로 보면 위와 같다. 한바퀴 돌면서 행렬을 하나씩 구하면서 결과적으로 우리가 원하는 $\tilde{A}$를 구할 수 있게 된다.
예제를 통해서 살펴보자.

우리는 3차원에서 4차원으로 linear mapping을 할 때 transformation matrix 인 $A_{\Phi}$를 알고 있다(2.117). 이 때 $A_{\Phi}$ 는 canonical basis 인 $B, C$에 의한 것이다. $\tilde{B}$에서 $B$로 갈 때 coordinate은 $B$가 표준기저라 그대로 $\tilde{B}$로 쉽게 구할 수 있고,$T$역시 마찬가지로 $C$가 표준기저라 coordinate를 쉽게 구할 수 있다. 이제 구한 것들을 다 곱하면 새로운 기저에서의 transformation matix $\tilde{A}_{\Phi}$를 구할 수 있다.

'수학' 카테고리의 다른 글
| Linear Algebra(5) (0) | 2020.04.26 |
|---|---|
| Linear Algebra(4) (0) | 2020.04.26 |
| Linear Algebra(3) (0) | 2020.04.06 |
| Linear Algebra(2) (0) | 2020.03.30 |
| Linear Algebra(1) (0) | 2020.03.29 |




댓글