Linear Algebra(4)에서는 Image, Kernel, Affine Space, Inner Product, Length, Angle, Orthonormal Basis에 대해 알아본다.
Image와 Kernel.

이미지와 커널의 정의는 위와 같다. 우선 kernel 또는 null space라 부르는 녀석은 전에 homogeneous system에서 $ax = 0$의 solution을 구했을 때를 생각하면 된다. 이 때 솔루션이 나타내는 그 영역이 곧 kernel space라고 생각하면 된다.
image(column space)는 매핑을 하였을 때 매핑되는 새로운 벡터스페이스의 서브스페이스를 말한다다. 즉 치역들이 있는 공간이라고 생각하면 된다. 또한 성질 중에 $V, W$가 각각 $n$, $m$차원 일 때, transformation matrix $A$의 랭크 즉 $rk(A) = dim(Image(\Phi))$라는 성질이 있다. 아래의 그림을 보면 이미지와 커널의 직관적인 이해가 가능하다.

예제를 한번 풀어보자.

보니까 매핑 $\Phi$는 4차원에서 2차원으로의 매핑이다.

Rank-Nulity Theorem

Affine Spaces.
원점으로부터 offset을 가지는 spaces를 말하며 이 spaces는 더이상 subspaces가 아니다.


affine subspace는 (2.131)과 같이 나타낸다. 이를 $parametric \ equation$이라고 한다.
모양이 영.. 회귀식 같은 느낌이다. !?!?
그림을 통해 살펴보자.

$u$라는 공간은 결국 $U$라는 $u$의 연장선 산의 일부분이므로 subspace인데, 여기서 $u$ 에 벡터 $x_{0}$를 더하고 $u$에 상수$\lambda$배를 한 새로운 subspace $L$을 affine subspace라 한다. 원점을 지나지 않게 된다.
Norm. 벡터의 길이를 나타냄.

보통 원소들의 총합이라 해서 Manhattan Norm과 제곱합이라 해서 Euclidean Norm을 구한다. 아래와 같다.


Inner product
내적의 특별한 형태로써 각 원소들을 곱한 것의 합으로 나타내는 Dot product가 있다.

General inner product의 bilinear mapping은 두 arguments의 매핑이며 아래의 성질을 갖는다. 분배법칙처럼 생각하면 된다.

linear하기 때문에 mapping에서 상수는 앞으로 뺄 수가 있다.
bilinear mapping $\Omega$가 symmetric하고 positive definite을 만족하면 $V$에 대한 inner product라고 정의한다.

Angle.
코사인 유사도를 가지고 두 벡터 사이의 각을 구할 수 있다.

$w$는 각도를 나타낸다. 두 벡터 각각 놈의 곱 분의 두 벡터의 내적 값이 벡터 사이의 코사인 각이라 한다. 그리고 이 각이 90도를 이루면 orthogonality라 하여 직교한다고 한다.

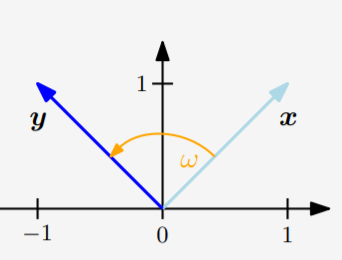
그 중에서도 두 벡터의 놈이 1이면 그 때의 벡터를 unit vector라고 하며, 두 벡터를 orthonomal(정규직교)하다고 한다.
Orthogonal Matrix는 정방행렬 $A$의 컬럼들이 모두 orthonomal인 애들이면 아래의 식을 만족한다.

orthonomal basis에 대해 자세히 알아보자.
n 차원의 벡터스페이스에서 는 n개의 기저벡터가 필요하겠지. 또 우리는 length와 angle을 구할 수도 있었다. 이제 각 기저벡터의 길이가 1이고 기저 벡터들이 orthogonal한 특별한 케이스를 살펴볼 것이다. 이 때 basis를 우리는 orthonormal basis라 한다.

(3.33)은 각기 다른 기저 벡터들 간의 내적값은 0이고, 각 기저벡터의 내적값은 1이라는 것이다.

위의 예시 처럼 $b_{1}, b_{2}$는 모두 기저벡터에 속한다. 또한 각각 길이가 1이고, 이 둘의 내적은 0이므로 orthonormal basis라고 할 수 있다.


위의 식이 의미하는 바는 다음과 같다. 우선 $x$는 벡터스페이스 $V$의 벡터를 말한다. 이를 $V$에 서브 스페이스인 $U$의 기저인 $b$들과 orthogonal basis인 $b^{\perp}$ 들의 선형결합으로 모두 표현이 가능하다.
직교인애들 + 직교아닌 애들 = original vector space공간을 표현 할 수 있다. 그래서 $U$가 $M$차원이면 $U^{\perp}$는 $V$의 차원인 $D$에서 $M$을 뺀 $D-M$차원이다. $\perp$ 는 orthogonal 의 notation이다.

위의 그림에서 $U$라는 sub spaces에서 2차원으로 공간이 표현되는데, 이 때 2차원의 벡터들과 orthogonal한 벡터들을 $w$와 같이 표현함으로써 3차원 공간을 표현할 수 있게 됨. 만약 original vector space $V$가 3차원이라면 $U$라는 subspace와 $w \in W$ space로 $V$를 완벽하게 표현할 수 있다.
'수학' 카테고리의 다른 글
| Linear Algebra(6) (0) | 2020.04.27 |
|---|---|
| Linear Algebra(5) (0) | 2020.04.26 |
| Linear Algebra(3)_linear Mappings (0) | 2020.04.07 |
| Linear Algebra(3) (0) | 2020.04.06 |
| Linear Algebra(2) (0) | 2020.03.30 |




댓글