Linear Algebra의 중심적인 역할을 하는게 행렬(Matrics)이다. 이 행렬은 선형 연립 방정식을 잘 표현해주고, linear function(linear mappings)역시 잘 표현해준다.
행렬을 정의해보자.
$m,n \in \mathbb{N}$ 즉 $m,n$이 정수일 때, 행렬 $A$ 는 $a_{ij}, i=1, ... ,m , j=1, ... ,n $ 인 $a_{ij}$ 원소들의 $mn$튜플이라고 할 수 있다. 이 때 $a_{ij}$는 $m$행, $n$열의 구성으로 사각형 형태로 정렬되어 있다. 아래 그림을 보면 바로 알 수 있다.
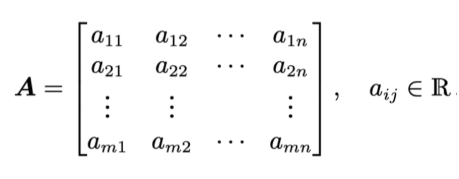
$(1,n)$을 행 벡터(row vector)라하고 $(m,1)$를 열 벡터(column vector)라고 한다. $\mathbb{R}^{m \times n}$는 $(m, n)$행렬의 모든 값들의 집합을 의미한다.
$A \in \mathbb{R}^{mn}$이라하면 행렬의 모든 $n$열들을 stacking함으로써 하나의 긴 벡터로 만든 것을 의미한다. 아래의 그림을 참고하자. 이 과정을 reshape라 한다. 쉽게 말해 한 줄로 이어 붙이는 것이다. 굳이 왜하는지는 잘 모르겠다. 계산상 편의? notation을 위함?...

행렬의 덧셈과 곱셈에 대해 살펴보자. 이부분은 정의만 보고 넘어가도록 하였다.
$A \in \mathbb{R}^{m \times n}$ ,$B \in \mathbb{R}^{m \times n}$일 때, 이 두 행렬의 합은 아래의 그림과 같다. 각각 동일한 위치의 원소들끼리의 합으로 새로운 행렬을 탄생시킬 수 있다. 행렬의 크기는 두 행렬이 동일해야한다.
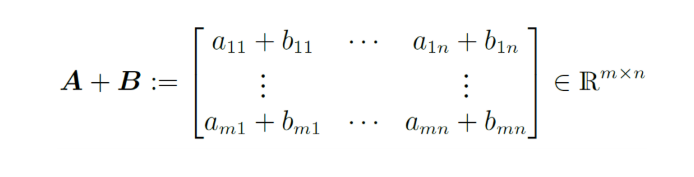
행렬의 곱셈은 $A \in \mathbb{R}^{m \times n} , B \in \mathbb{n \times k}$ 일 때, $c_{ij}$는 $AB$의 결과 행렬의 원소들이다. 즉 $ C = AB \in \mathbb{R}^{m \times k} $의 원소를 말한다. 아래의 sumation으로 정의할 수 있다.

교재에선 행렬의 곱은 "neighboring" 차원의 곱으로 곱해질 수 있다고 한다. 즉 곱셈에서 (앞 행렬의 열의 수 X 뒤 행렬의 행의 수)인 행렬로 결과값이 출력된다는 말이다.
행렬 곱셈 중 아다마르 곱(Hadamard product)라고 같은 위치에 있는 원소끼리 곱하는 연산도 있긴하다. 하지만 여기선 다루지 않는다.
다음은 행렬 곱셈에 대한 문제인데 행렬 $A, B$의 위치를 바꾸어 곱셈을 진행하면 다른 결과가 나온다는 것을 쉽게 알 수 있다.
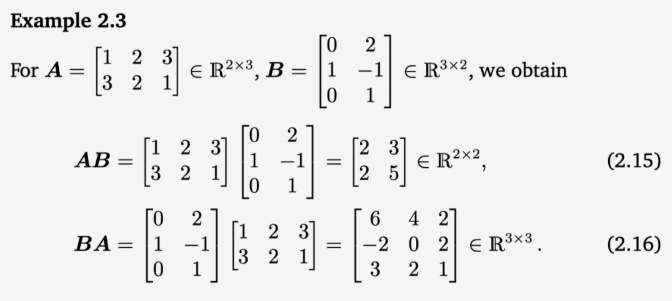
Identity matrix(항등행렬)
항등원이라하면 연산을 거치면 결과로 자기자신을 나오게 해주는 수를 말하는데, 곱셈의 1, 덧셈의 0이 이에 해당한다. 행렬 역시 항등원을 가지고 있는데 덧셈에 대하여 영행렬(원소가 전부 0인 행렬),곱셈에 대하여 항등행렬( $\mathbb{R}^{n \times n}$ , $a_{ii}$ 가 모두 1인 행렬)이 있다. 아래의 그림은 항등행렬을 나타낸다. $I$ 밑에 $n$은 행 또는 열의 크기를 나타낸다. 왜냐하면 항등행렬은 열의 크기와 행의 크기가 같기 때문에 하나만 나타내줘도 된다.

행렬이 가지는 성질에 대해 알아보자.
-Associativity
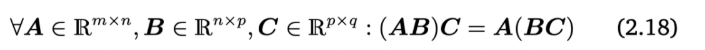
$\forall$의 의미는 임의의라는 뜻이다. 즉 '모든'이라고 해석함도 동일하다고 볼 수 있다. 아무튼 행렬의 곱에서 나열된 행렬들의 위치를 고정한채 계산순서를 변경해도 결과값은 동일하다는 내용이다. 결합법칙.
-Distrubutivity

분배법칙이 성립한다는 내용이다. 다만 주의할점은 괄호 밖에 있는 행렬이 괄호 속에 있는 행렬과 곱할 때 위치를 그대로 유지하면서 곱해줘야한다는 점이다.
-Multiplication with the identity matrix

앞서 언급한 항등행렬과의 곱은 자기자신이 나오게 한다. 실수 곱하기 1은 자기자신이 나오는 것과 동일한 개념이다. 2.20에서 유의할 점은 $I_{m} \neq l_{n} $이다.
- Inverse(역행렬)
행렬 $A \in \mathbb{R}^{n \times n}$ 를 고려해보자. 행렬 $B \in \mathbb{R}^{n \times n}$이 $AB = I_{n} = BA$라는 특징을 가진다.
$B \in \mathbb{R}^{n \times n}$ 는 $A$ 의 역행렬(Inverse)라고 부르고 $A^{-1}$과 같이 표기한다.
모든 행렬이 역행렬을 가지는 것은 아니다. 역행렬이 존재하면 우리는 이것을 inverse뿐만 아니라 regular/invertible/non-singular 행렬이라고 부른다. 그렇지 않은 행렬은 singular/non-invertible 라고 부른다.
아래의 식처럼 좀 전의 $I$ 가 $AB$라는 점을 이용하여 표현할 수 있다. ($C$는 $A$의 역행렬이라는 가정을 해야한다.)

역행렬에 대해 더 알아보자.
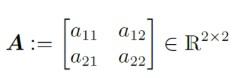
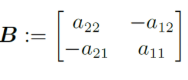
위와 같이 $A, B$가 있다고 하자. 이 둘의 곱은 아래와 같이 전개될 수 있다.

$a_{11}a_{22} - a_{12}a_{21}$은 우변에서 처럼 costant(상수)로 표현할 수 있다.
자 이제 이 상수를 양변에 나눠주면 $A^{-1}$를 구하는 행렬식이 나오게 된다.
아래의 빨간색으로 표기한 부분이 0이냐 아니야를 가지고 판별식(determinant)이라고 하는데 이게 0이면 역행렬이 존재하지 않고, 0이 아니면 역행렬이 존재하는 행렬로 판별할 수 있다.

Transpose(전치행렬)
$A \in \mathbb{R}^{m \times n } $와 $B \in \mathbb{R}^{m \times n } $ 모든 $i, j$에 대하여 $b_{ij} = a_{ji}$이면 $B$를 $A$의 전치행렬이라고 부른다.

Symmetric matrix(대칭행렬)
대칭행렬이라고 해서 왼쪽위에서 오른쪽 아래를 가로지르는 원소들(대각원소)을 기준으로 양쪽의 원소들이 서로 대칭을 이룬다하여 대칭행렬이라 한다. $A = A^{T}$로 표현할 수 있고, 만약에 $A$가 역행렬이 존재한다면 다음의 특징을 갖는다.

대칭행렬끼리의 덧셈은 늘 대칭행렬 결과를 나타내지만, 대칭행렬끼리의 곱에선 일반적으로 대칭행렬이 나타나지 않는다.
역행렬과 전치행렬이 가진 중요한 특징을 알아보자

막상 한번 보면 어렵지 않게 외울 수 있다. 직접 예시를 들고 계산하는 것도 좋다. 특히 마지막에 $(AB)^{T} = B^{T}A^{T}$ 가 중요하다.
스칼라 곱
행렬 $A \in \mathbb{R}^{m \times n}$ 이 있고, 스칼라 값 $\lambda \in \mathbb{R}$ 이 있다. 이 둘의 곱 $\lambda A = K$ , $K_{ij} = \lambda a_{ij}$로 나타낸다.
상수 $ \lambda, \psi \in \mathbb{R} $일 때, 아래의 특징들을 가진다.
- Associativity

스칼라와의 결합법칙

스칼라는 막돌아다녀도 된다.

스칼라 상수 값은 전치를 해도 자기 자신이다. 모든 $\mathbb{R}$에 대해서 말이다.
- Distributivity

스칼라를 분배하는 것도 역시 가능하다.
- Compact representations of systems of linear equations
선형 연립 방정식의 콤팩트한 표현.
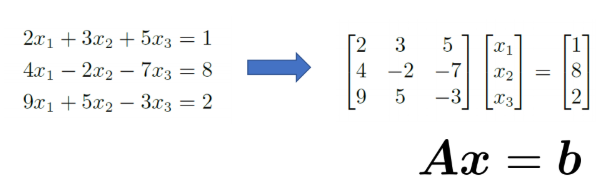
여기서 $Ax$는 행렬 $A$의 column들의 하나의 선형결합이다. 차근차근 알아가보도록 하자.
- Solving systems of linear equations
선형 연립 방정식의 일반적인 형태는 다음과 같다.
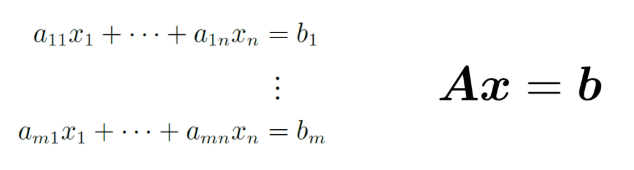
앞장에서 햄버거 문제를 통해 잠깐 말했듯 우리는 이미 $a_{ij} \in \mathbb{$}, b_{ij} \in \mathbb{R}$ 상수를 이미 알고 있고, 우리가 몰라서 알고 싶은 것은 $x_{i}$ 들이다.
-Particular and general solution
특정해, 일반해에 대해서 알아보자. 우선 다음의 연립방정식을 살펴보자. 위에서 본 형태와 같이 표현된 방정식이다.
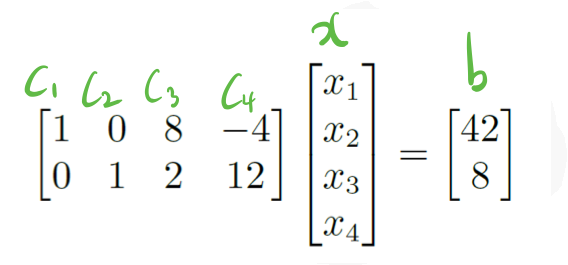
우선 위의 식을

로 나타낼 수 있다.
쉽게 쉽게 생각해보자. 여기서 지금 방정식은 2개이고 미지수는 4개이다. 그렇다 무수히 많은 해가 존재하는 연립방정식이다. 아래 처럼 식으로 표현해보면 직관적으로 해를 구해볼 수 있다.
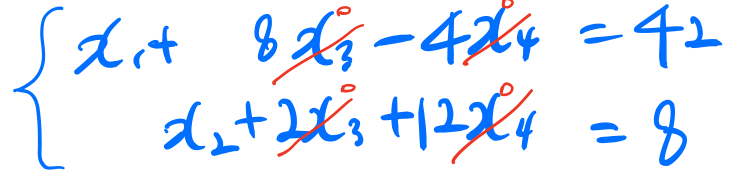
두 식에 공통으로 들어있는 $x_{3}, x_{4}$에 0을 넣어버리자. 그랬더니 $[42,8,0,0]^{T}$이라는 해를 손쉽에 얻을 수 있게 됐다. 모로가도 이렇게 해를 얻으면 되는 것이다.
우리는 $[42,8,0,0]^{T}$ particular/special solution 이라고 주어진 식을 만족해주는 하나의 특정해를 찾았다고 할 수 있다.
자 이번에는 left-hand side를 0으로 만듦으로써 다른 모든 해를 더 찾아보도록 하자. left-hand side를 0 으로 한다는 것은 등호를 기준으로 0이 되는 식을 한쪽에 둔 그런 식을 만든다는 것이다. 예) $ax +b = 0$
위에서$c_{1}x_{1} + c_{2}x_{2} + c_{3}x_{3} + c_{4}x_{4} = b$ 같이 나타낼 수 있었는데, 이를 벡터로 다시 나타내보면 $cx = b$로 나타낼 수 있고, 우리가 아까 구한 해$[42,8,0,0]^{T}$를 $x^{*}$라고 할 때, $cx^{*} = b$로 나타낼 수 있다.
자 여기서 등식이 0이 성립하는 $cx^{sth} = 0$ 을 만족하는 $x^{sth}$을 찾는다면 우리는 다음과 같이 나타낼 수 있다.
$c(x^{*} + x^{sth}) = b $ . 왜냐하면 $c$를 분배해보면 결국에는 $cx^{*} = b$ 형태가 되기 때문에 $x^{sth}$가 0이 되는 해를 찾는 것도 또 해를 찾는 하나의 방법이 되는 것이다.
$c$의 세번째 열은 첫번째, 두번째 열의 각각 상수 곱의 합으로 나타낼 수 있다 아래그림처럼.

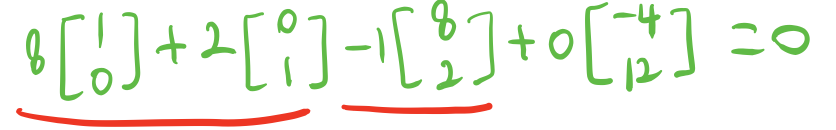
즉, 첫번째 두번째 열의 합을 세번째 열로 빼버리고 마지막 네번째 열은 0을 둬서 전체적으로 0벡터를 만드는 것이다. 여기서 중요한 포인트가 있다.

결과적으로 우리가 구한 해에 $\lambda_{1}$에 어떠한 상수를 넣어 곱해도 결과가 영벡터를 내뱉어서 식이 만족하는 것을 알 수 있다.
$x_{4}$에 0을 넣어 만족시킨 해를 찾았다면 이번에는 $x_{3}$에 0을 넣어 만족시키는 해를 찾아보면 아래처럼 나타낼 수 있다.

결과적으로 다음과 같이 표현할 수 있다.

이는 다시 $cx = b$, $x^{*}+c\lambda_{1}x_{1}$
정리해보면 일반적으로 particular, general solution을 찾는 접근방법은
$Ax=b$ 형식으로 particular 해를 구한다.
그 다음 $Ax = 0$에 대한 모든 해를 구한다. <- homogeneous system 이라고 한다.
그리고 이러한 해들을 통해 해를 식(2.43)처럼 잘 나타내 주면 된다.
- Elementary transformations
이 부분은 아마 연립방정식을 풀어본 사람이라면 장황한 위의 설명보다 쉽게 이해할 수 있을 것이다. Elementary transformations는 주어진 방정식들의 해는 유지하되 방정식을 좀 더 쉬운 형태로 변형하면서 해를 찾아나가는 방법이다.
1. 두개의 방정식을 서로 교환한다.
2. 각 방정식에 상수를 곱하면서, $\lambda \in \mathbb{R} \setminus \left \{ 0 \right \} $ 0말고;;
3. 두 방정식을 더하면서 차차 심플하게 변형시켜나간다.
잔말 말고 문제를 풀어보도록 하자.
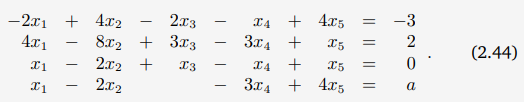
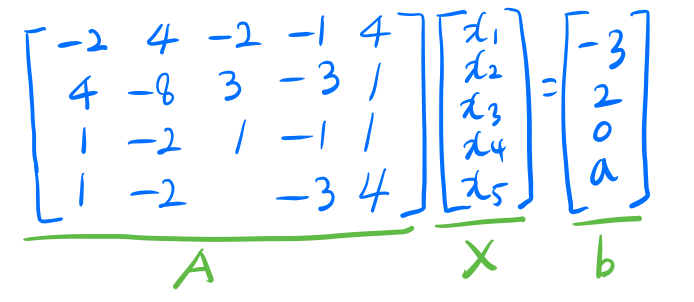
위의 연립방정식을 다른 방식으로 표기하였다.
이제 [A | b] 의 형태로 변환해서 1,2,3을 떠올리면서 계산해보자.

직접해보면 좋지만 귀찮으면 순서에 맞게 흘러가는 느낌을 느끼면된다. 계산이 모두 끝나면 아래와 같은 방정식으로 최종적으로 표현할 수 있다.

이러한 꼴을 REF라고 한다. 이에 대한 규칙은 뒤에 설명한다. 간략하게만 말하면 계산을 쉽게 해주는 방법이라는 것이다. 소거하기 좋게.
계산하기 좋게 정리를 했으면 이제 위에서 general solution을 구하기 위한 2가지 스텝을 밟아보자.

우선 위와 같이 particular solution을 구하는 것이다. 시작은 $x_{5}$를 0으로 두고 6번 식에 대입하면서 해를 찾는 것이다. particular solution을 구했다면 이제 homogeneous system으로 해를 구해보자.

$Ax = 0$로 만들어주기 위해 6번의 우항을 0으로 통일 시켜주고, 냅다 $x_{3}, x_{4}, x_{5}$에 0을 넣어준다. 그다음에는 $x_{5}$에 1을 한 번 넣어줌으로써 두 개의 해를 얻게 되는데.
이제 general solution으로 표현해보자.

위의 글씨가 너무 불순하여, 아래의 것을 보자.
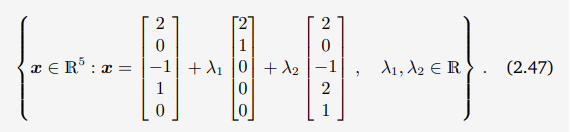
general solution은 유일한 해의 형태는 아니다. 어떤 변수를 고정하고 구했느냐에 따라서, homogeneous system에서도 그렇고 달라질 수 있다. 하지만 general solution로 해를 찾게 되면 같은 벡터들의 집합을 표현하게 된다.
- staircase structure, pivot, pivot columns
위에서 Elementary transformation 할 때 6번 연립방정식을 가져와서 한 번에 보면, 아래와 같다.

피벗은 행에서 가장 왼쪽에 있는 0이 아닌 값이고 바로 위에 행보다 무조건 오른쪽에 위치해야한다. 이러한 피벗을 포함하는 열을 피벗컬럼이라고하고, 위의 구조를 staircase라 하며, row-echelon matrix. 기약행사다리꼴행렬의 형태라고 할 수 있다.
- row-echelon form
행의 모든 값이 0이면 가장 아래의 행으로 가고, 하나도 0이 아니면 가장 위에 행에 위치해야한다.
피벗이 있는 변수를 basic variables라 하고 나머지 변수들을 free variables라고 한다.
row-echelon form는 particular solution을 훨씬 더 쉽게 찾을 수 있게 해준다.
reduced row-echelon form은 더욱 더 쉽게 해를 구할 수 있게 해주는데, 기존의 row-echelon form의 모든 피벗컬럼들에 대해서 피벗을 제외한 해당 열의 다른 원소가 모두 0이면 조건을 만족한다.

위의 형태가 reduced row-echelon form형태이다. 이것으로부터 particular solution을 순식간에 구할 수 있는데, 우선 free variables를 0으로 두면 나머지 값을 쉽게 구할 수 있다.

- Gaussian elimination
가우스 소거법이라해서 위의 reduced row-echelon form 을 만드는 방법을 말한다.

위의 행렬이 reduced row-echelon form 인지 판단하고, 일반해를 구해보자.
우선 row-echelon form형태를 띄고 있으며, 피벗 컬럼의 경우 피벗을 제외한 원소들이 모두 0이기 때문에 이 행렬은 reduced row-echelon form 을 만족한다.
이 행렬 시스템 자체가 homogeneous 형태이기 때문에 particular solution을 구할 필요는 없다. 바로 $Ax=0$으로 해를 구하면 된다.
free variables를 0으로 두는 것으로 해를 구해나가면 되는데,
$x_{5}$를0, $x_{2}$를 1로 두는 경우와 $x_{5}$를 1, $x_{2}$를 0으로 두는 경우에서 해를 구해보면 (kick-out이라 한다.)
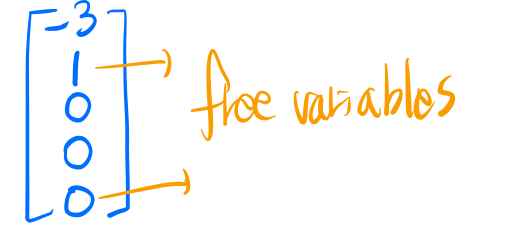
$x_{5}$를0, $x_{2}$를 1로 두는 경우의 해이고, -1을 곱한 값이 책에는 나왔는데 딱히 상관은 없다. $x_{5}$에 1을 두는 경우의 해도 구하면 결과적으로 아래와 같은 general solution을 구할 수 있다.

최종적으로 위와 같은 general solution 을 구할 수 있다.
- Minus-1 Trick
reduced row-echelon form matrix에서 손쉽게 해를 구하는 방법으로 free variable column자리에 대각원소에 해당하는 곳에 -1, 나머지는 0인 행을 삽입하여 그 열들의 선형 결합으로 general solution을 구할 수 있다.


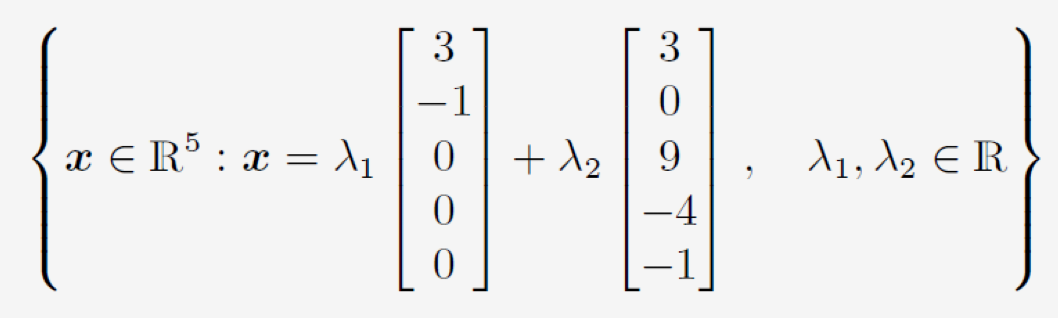
자주색이 칠해진 열들의 선형결합으로 general solution을 구할 수 있다.
- calculating inverse
어떠한 행렬 $A$의 역행렬을 구한다는 것은 $AX = I$ 라는 system of equation을 푸는 것과 같다. 즉 $[A | I]$의 시스템을 $[I | B]$ 의 형태로 바꾸어 줌으로써 결과적으로 $B = A^{-1}$라는 것을 앎으로써 해를 구하는 것이다.




위의 계산과정은 기존의 행렬을 reduced row-echelon form으로 만드는 가우스 소거법을 사용하여 단위행렬로 변형하면서 각 방정식의 계산을 오른쪽의 기존의 단위행렬에도 똑같이 적용하면서 만든 결과 역행렬을 얻는 과정을 나타낸다.
가우스 소거법은 왼쪽열부터 오른쪽열로 위에서 아래로 하나씩 변형시켜주면서 나가면 실수를 줄일 수 있다. 순서를 마구 바꾸면서 하다보면 실수가 나서 해온 계산과정을 전부 다시해야하기 때문에 한 번할 때 천천히 마무리 하는게 좋다.
- vector space
벡터들이 살고 있는 구조적 공간을 말한다. 벡터라는 것은 벡터끼리 더했을 때 또 벡터값이 나오고, 스칼라와의 곱을 통해서도 다시 원래의 형태와 같은 형태의 결과값을 나올 때의 objects를 말한다. elements와 oeration의 형태로 정의를 하고 있다.
아래의 정의는 Group을 정의하는 4가지 성질에 대한 설명이다.

1. 연산에 대해 닫혀있는지(연산후의 값이 여전히 같은 그룹에 속해 있는지)
2. 결합법칙이 성립하는지.
3.연산에 대해 항등원역할이 존재하는지.
4.역원이 존재하는지($x^{-1}$).
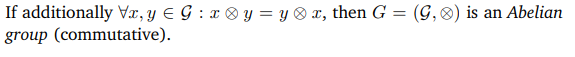
교환법칙까지 성립하면 Abelian group에 속하게 된다.
아래는 다른 집단에 대해서 group인지 아닌지를 알려주는 내용이다.

가장 아래에 $\mathbb{R}^{n \times n}$의 경우 inverse가 존재하지 않을 경우에는 group이 아닌데, inverse가 존재하는 경우에는 $(\mathbb{R}^{n \times n}, \dot)$은 group이라 할 수 있다.. 우리는 특별히 이러한 그룹을 general linear group GL($n$,$\mathbb{R}$)라고 하지만 곱셈에 대해 교환법칙이 성립하지 않으므로 Abelian은 아니다.
지금까지는 inner operation에 대해 알아 보았다. inner operation은 동일한 집합내의 값들에 대한 연산을 가지고 했다면 outer operation은 다른 집합에 속한 것들의 연산에 대해 group인지 판단하는 것이다.
- vator space
inner operation과 outer operation 둘 다 고려하여 정의를 해준다.
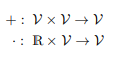
덧셈은 inner 곱셈은 스칼라와 같이 outer operation 으로 정의한다.
$V = \mathbb{R}^{n}, n \in \mathbb{N}$ 는 아래의 두 operations에 대해 vector space라고 할 수 있다.
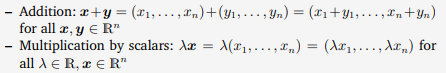
$V = \mathbb{R}^{m \times n}, m,n \in \mathbb{N}$ 역시 vector space로 정의 가능하다.

벡터 안의 벡터. vector subspace를 정의하는 글.


2번 . $U$는 a,b에 대해 닫혀 있어야 한다.
아래의 그림은 $\mathbb{R}^{2}$에 대한 vector subspace공간에 대해 닫힘여부를 보여준다.
결과는 A, B, C모두 닫혀 있지 않고, D만 닫혀 있다. 기본적으로 vector subspace는 자기자신과 0벡터를 가져야하기 때문에 두번째 B vector는 subspace가 될 수 없고, A와 같은 경우는 스칼라곱에 의하여 subspace범위를 벗어나게 되고, C의 경우 outer operation에 대해선 닫혀있지만 inner operation에 의해 닫혀있게 된다.
inhomogeneous system 에서 $ Ax = b, b \neq 0$ 이면 $\mathbb{R}^{n}$의 subspace가 아니다. subspace들 사이의 intersection 역시 subspace에 속한다.

Mathematics for Machine Learning
Companion webpage to the book “Mathematics for Machine Learning”. Copyright 2020 by Marc Peter Deisenroth, A. Aldo Faisal, and Cheng Soon Ong. Published by Cambridge University Press.
mml-book.github.io
'수학' 카테고리의 다른 글
| Linear Algebra(5) (0) | 2020.04.26 |
|---|---|
| Linear Algebra(4) (0) | 2020.04.26 |
| Linear Algebra(3)_linear Mappings (0) | 2020.04.07 |
| Linear Algebra(3) (0) | 2020.04.06 |
| Linear Algebra(1) (0) | 2020.03.29 |




댓글