머신러닝을 위한 수학지식에 대해 공부를 해보자. 앞으로 다음과 관련된 수학 지식을 알아본다.{ 선형대수학-데이터분석, 확률 및 통계-데이터과학, 최적화-모델학습} . 기초적이고 기본적인 학습이므로 높은 수준의 수학적 지식을 원하는 사람은 별로 도움이 안 될 것이다.(이 블로그 모든 다른 챕터에 대하여)
Linear Algebra에 대한 것부터 시작해보자. 본 교재에서 사용하는 표기법(Notation)은 아래의 그림과 같다.

표기법에 나와 있는 기호들은 다른 교재나 논문에서도 공통적으로 사용되기 때문에 잘 알아두자.

머신러닝을 위한 기본지식 중 가장 근본적인 수학 지식을 쌓을 것이다. 위의 그림처럼 왼쪽 아래에 우리가 공부할 선형대수가 놓여있다. 수학적 지식과 이를 활용한 알고리즘들로 우리는 훗날 머신러닝에 대한 이해도를 많이 높힐 수 있을 것이다.
Algebra
한글로 직역하면 대수학이다. 이 학문은 수학적 기호와 이러한 기호들을 조작하는 규칙들에 관한 학문이다.
Linear algebra
한글로 직역하면 선형대수학이다. 벡터들을 조작하는 특정 규칙들에 대한 연구를 한다. 물리학적 관점에서는 "geometric vector"라 하여 $\vec{a}, \vec{b}$ 와 같이 표기한다. 수학적 관점에서는 벡터에대한 좀더 일반적인 개념을 다루고 bold체를 사용하여 $ x, \ y$로 나타낸다.
Vector
벡터라 하면 크기와 방향을 나타내는 object로써 같은 벡터끼리 더하거나 혹은 벡터에 스칼라 값을 곱했을 때 결과값이 원래 타입과 동일한 벡터로 출력되면 벡터라 한다.

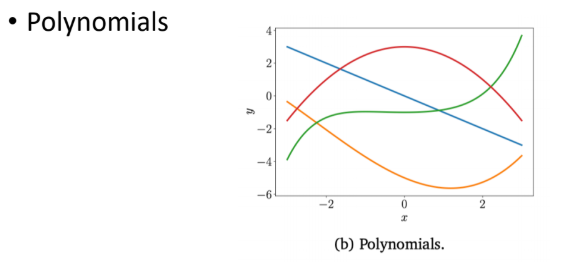
기하학적으로 벡터를 나타낼수도 있고, 다항식처럼 그래프 상에 나타낼 수 있다.

위의 그림은 $a$라는 벡터를 실수 1,2,3 을 가진 3차원 벡터라고 한다. 원소들의 개수에 따라 demension이 결정된다. 이 때 1,2,3은 순서를 가지고 있어야하며 이러한 원소들 무한개가 아닌 유한개여야 한다. 이러한 원소들은 실수로 이뤄진 3차원 벡터공간에 있다. 그 표시가 $\mathbb{R}^{3}$ 이다.
$x_{1}$ 은 1 로 나타낼 수 있다.
만약 벡터 $ x, y, z $ 가 있고 각각 크기가 $m , n, p$라고 한다면 stacking vector라 하여 $x, y, z$들에 대해서 $a$라고 block vector라 하여 다음과 같이 나타낼 수 있다.
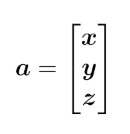
그리하여 $a$ 의 크기는 $m + n + p $로써 다음과 같이 나타낼 수 있다.
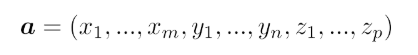
명확한 정의나 역사, 증명 등은 생략하고 실생활에 어떻게 적용되는지를 보자.
Systems of linear equations 라고 쉽게 말해 연립방정식의 해를 구하는 문제이다. 여기서는 해를 구하지 않고 실세계 응용에 대한 것만 알고 넘어간다.

교재에 나오는 문제이다. 이 문제는 한 회사가 제품을 생산하려고 하는데 제한된 자원을 가지고 최대한 활용하여 제품을 만들려면 생산계획을 어떻게 짜야할까라는 문제이다. 쉽게말해서 여러가지 종류의 햄버거를 만드는데 우리가 가진 자원(빵100개 , 패티 70개, 야채 120개, 등)을 최대한 활용하여 햄버거를 몇개나 만들 수 있을까라는 문제를 해결하는 것이다.
저 문제는 실제 문제를 해결한다고 생각하고 풀어보면 꽤나 재밌게 풀 수 있다. 쉽게 설명하기 위해서 company는 맥도날드라하고, products는 햄버거고, resource는 햄버거에 들어갈 재료라고 해보자.
$N_{n}$ 은 $n$종류의 햄버거 $N$ 이라고 하고, $R_{m}$은 각각 햄버거에 들어가는 재료들이라 하자.
특정 햄버거 하나를 $N_{j}$라 하고, 그 햄버거$j$에 들어가는 재료$R_{i}$를 나타내는 것을 $a_{ij}$라 한다.
햄버거의 종류는 $j = 1,2, ... ,n$ 이 되고, 햄버거 재료는 $i = 1,2, ... ,m$이 된다.
이어서 $x_{j}$, $b_{i}$ 가 있는데 식 (2.3)의 가장 위의 방정식을 가지고 설명해보면 $b_{1}$란 모든 햄버거에 들어가는 특정 재료$a_{1j}$가 그 모든 햄버거 $N_{n}$에 각각 쇽쇽 들어가는 총 양이 얼마냐를 나타낸다. 쉽게 말해 특정 재료 R_{i}의 총 양이다.
여기서 우리가 이미 알고 있는게 뭔지 생각해보자. 우리가 알고 있는 것은 바로 각 햄버거가 필요로하는 재료가 얼만큼인지와 우리가 현재 가지고 있는 재료가 얼만큼인지 이다. 즉 우리는 이미 $a$와 $b$를 알고 있는 것이다. 우리는 $x$라고 하여 햄버거 개수를 최대 얼마나 만들 수 있는지를 모를 뿐이다.
훗날 우리는 아래와 같은 형식으로 만들게 되고 최적의 $x$ 값들을 구해내서 맥도날드에서 한정된 자원의 양을 토대로 만들 수 있는 최적의 종류별 햄버거 개수를 알아낼 수 있다.
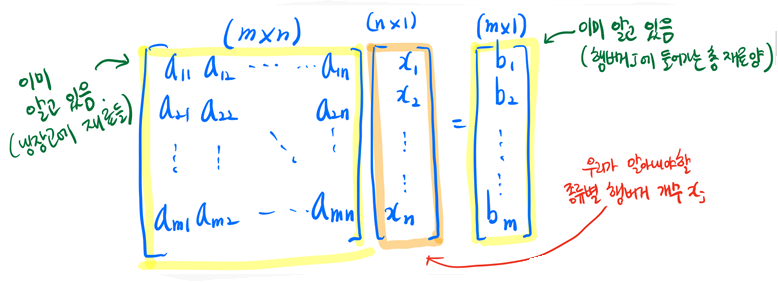
system of linear equation의 해를 구해보자. 이 때 세가지 형태로 해가 구해지니 그것은 1.해가없을때 2.해가 유일할 때 3.해가 무수히 많을 때이다.
1.해가 없을때. (no solution)

식 (1)과 (2)를 더하면 $2x_{1} + 3c_{3} = 5$가 되는데 이는 식 (3)의 좌변과는 동일하지만 우변 상수가 다른값을 가진다. 즉, 말이 안되므로 해가 없다라는 것을 알 수 있다.
2. 해가 유일할 때(unique solution)

식 (1)과 (2)를 더하면 $2x_{1} + 3c_{3} = 5$가 됨을 알 수 있다. 이 때, 식 (3)에 $x_{2}, x_{3}$이 각각 1이라 하면 식 (1)에 대입하면 $x_{1}$가 1이 됨을 알 수 있고, (1, 1, 1)이 해가 된다라는 것을 알 수 있고, 유일하다는 것도 판단해볼 수 있다.
3. 해가 무수히 많을 때(infinetely many solutions)

식 (1)과 (2)를 더하면 식 (3)이 되는데 $x_{1}, x_{3}$에 각각 1을 넣어줘도 되지만 양의 실수, 음의 실수 등등 조합을 통해서 얼마든지 많은 식을 만들어 낼 수 있다. 즉 해가 무수히 많다고 판단할 수 있다.
아래의 그림은 2개의 미지수를 포함한 두 1차함수를 2차원 그래프 상에 올려 놓은건데 두 직선의 교점을 알아 냄으로써 이 두 식을 만족하는 유일한 $x_{1}, x_{2}$를 알아낼 수 있다.

미지수가 3개일 때는 각 선형 방정식은 3차원 공간에서 하나의 평면으로 알아낼 수 있다. 해 집합은 평면, 직선, 한 점일 수 있고, 없을 수도 있다.
Mathematics for Machine Learning
Companion webpage to the book “Mathematics for Machine Learning”. Copyright 2020 by Marc Peter Deisenroth, A. Aldo Faisal, and Cheng Soon Ong. Published by Cambridge University Press.
mml-book.github.io
'수학' 카테고리의 다른 글
| Linear Algebra(5) (0) | 2020.04.26 |
|---|---|
| Linear Algebra(4) (0) | 2020.04.26 |
| Linear Algebra(3)_linear Mappings (0) | 2020.04.07 |
| Linear Algebra(3) (0) | 2020.04.06 |
| Linear Algebra(2) (0) | 2020.03.30 |




댓글